6. 一个长方形的宽为 x cm,长为 y cm,面积为 $ 24 cm^2 $。
(1) 求 y 与 x 之间的函数表达式;
(2) 当 $ x = 3 $ 时,长方形的长为多少厘米?
(1) 求 y 与 x 之间的函数表达式;
(2) 当 $ x = 3 $ 时,长方形的长为多少厘米?
答案:
(1)由题意可知y=$\frac{24}{x}$.
(2)当x=3时,y=$\frac{24}{3}$=8,即长方形的长为8 cm.
(1)由题意可知y=$\frac{24}{x}$.
(2)当x=3时,y=$\frac{24}{3}$=8,即长方形的长为8 cm.
7. 如图反映的过程是小涛从家出发,去菜地浇水,接着又去玉米地锄草,然后回家。其中 x 表示时间,y 表示小涛离家的距离。
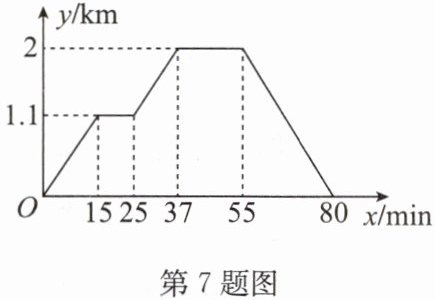
(1) 菜地离小涛家的距离是
(2) 菜地离玉米地的距离是
(3) 玉米地离小涛家的距离是

(1) 菜地离小涛家的距离是
1.1
km,小涛走到菜地用了15
min,小涛给菜地浇水用了10
min;(2) 菜地离玉米地的距离是
0.9
km,小涛给玉米地锄草用了18
min;(3) 玉米地离小涛家的距离是
2
km,小涛从玉米地走回家的平均速度是80 m/min
。
答案:
(1)1.1 15 10
(2)0.9 18
(3)2 80 m/min
(1)1.1 15 10
(2)0.9 18
(3)2 80 m/min
8. 甲、乙两车从 A 城出发匀速行驶至 B 城。在整个行驶过程中,甲、乙两车离开 A 城的距离 y(千米)与甲车行驶的时间 t(时)之间的函数关系如图所示。
(1) 在上述变化过程中,自变量是
(2) ①A,B 两城相距
②乙车比甲车晚出发
③乙车出发
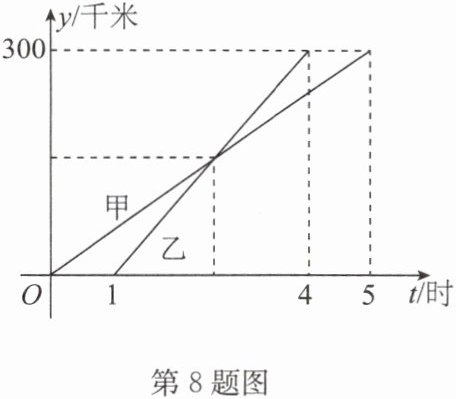
(1) 在上述变化过程中,自变量是
甲车行驶的时间t
。(2) ①A,B 两城相距
300
千米;②乙车比甲车晚出发
1
小时,乙
(填“甲”或“乙”)车先到达 B 城;③乙车出发
1.5
小时后追上甲车。
答案:
(1)甲车行驶的时间t
(2)①300 ②1 乙 ③1.5
(1)甲车行驶的时间t
(2)①300 ②1 乙 ③1.5
查看更多完整答案,请扫码查看


