1. 基本事实:
两边及其夹角
分别相等的两个三角形全等(简写成“边角边”或“SAS
”).
答案:
两边及其夹角 SAS
如图,在$\triangle ABC和\triangle DEF$中,$\left\{\begin{array}{l} AB= DE,\\ ∠B= ∠\underline{
$\therefore \triangle ABC\cong \triangle DEF$(
E
}\\ \underline{BC
}=\underline{EF
} \end{array}\right.$,$\therefore \triangle ABC\cong \triangle DEF$(
SAS
).
答案:
E BC EF SAS
1. 如图,$AB= AC,∠BAD= ∠CAD$,求证:$\triangle ABD\cong \triangle ACD.$
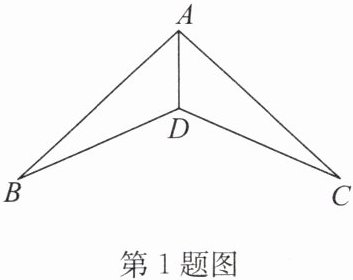

答案:
证明:在△ABD和△ACD中,{AB=AC,∠BAD=∠CAD,AD=AD,
∴△ABD≌△ACD(SAS).
∴△ABD≌△ACD(SAS).
2. 如图,点 B 在线段 AC 上,$BD// CE,AB= EC,DB= BC$. 求证:$AD= EB.$
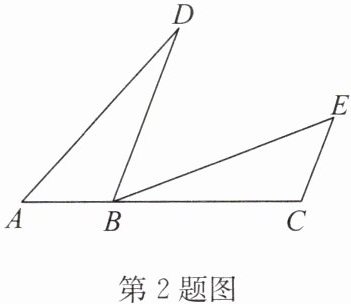

答案:
证明:
∵BD//CE,
∴∠ABD=∠C.
在△ABD和△ECB中,{AB=EC,∠ABD=∠C,DB=BC,
∴△ABD≌△ECB(SAS),
∴AD=EB.
∵BD//CE,
∴∠ABD=∠C.
在△ABD和△ECB中,{AB=EC,∠ABD=∠C,DB=BC,
∴△ABD≌△ECB(SAS),
∴AD=EB.
3. 如图,点 B,F,C,E 在同一条直线上,$AB= DE,BF= CE,AB// DE$. 求证:$AC= DF.$


答案:
证明:
∵AB//DE,
∴∠B=∠E.
∵BF=CE,
∴BF+FC=CE+FC,即BC=EF.
在△ABC和△DEF中,{AB=DE,∠B=∠E,BC=EF,
∴△ABC≌△DEF(SAS),
∴AC=DF.
∵AB//DE,
∴∠B=∠E.
∵BF=CE,
∴BF+FC=CE+FC,即BC=EF.
在△ABC和△DEF中,{AB=DE,∠B=∠E,BC=EF,
∴△ABC≌△DEF(SAS),
∴AC=DF.
查看更多完整答案,请扫码查看


