验证勾股定理,通常采用
面积
法,即将图形的面积“计算两次”.
答案:
面积
1. 若一个等腰三角形的腰长为5,底边长为6,则底边上的高为 (
A.4
B.3
C.5
D.6
A
)A.4
B.3
C.5
D.6
答案:
A
2. 如图,在四边形ABCD中,$∠DAB= ∠BCD= 90^{\circ }$,分别以四边形ABCD的四条边为边长向外作四个正方形,面积分别为$S_{1},S_{2},$$S_{3},S_{4}$. 若$S_{1}= 48,S_{2}+S_{3}= 135$,则$S_{4}$的值是 (
A.183
B.87
C.119
D.81
B
)A.183
B.87
C.119
D.81
答案:
B
3. 如图,图①②均由四个全等的直角三角形拼接而成,且它们的两条直角边长分别为a,b,斜边长为c,$a>b$. 请选择一个你喜欢的图形,利用等面积法验证勾股定理.


答案:
解:答案不唯一,如选择题图②,验证如下:
∵S大正方形=c²,S大正方形=4S三角形+S小正方形=4×$\frac{1}{2}$ab+(a-b)²,
∴c²=4×$\frac{1}{2}$ab+(a-b)²,
整理,得c²=2ab+a²-2ab+b²,即c²=a²+b².
∵S大正方形=c²,S大正方形=4S三角形+S小正方形=4×$\frac{1}{2}$ab+(a-b)²,
∴c²=4×$\frac{1}{2}$ab+(a-b)²,
整理,得c²=2ab+a²-2ab+b²,即c²=a²+b².
4. 如图,把一个直立的火柴盒放倒,请你用不同的方法计算梯形ACED的面积,验证勾股定理.(设火柴盒截面宽为a,长为b,对角线长为c)
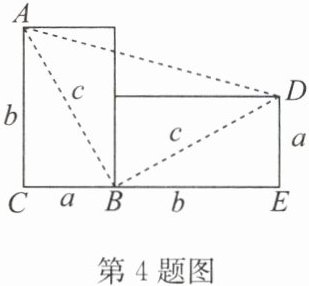

答案:
解:依题意,四边形ACED为直角梯形,△BDA为等腰直角三角形,Rt△ABC和Rt△BDE的形状和大小完全一样.
设梯形ACED的面积为S,则S=$\frac{1}{2}$(a+b)(a+b)=$\frac{1}{2}$(a²+b²)+ab,
又S=S△BDA+2S△ABC=$\frac{1}{2}$c²+2×$\frac{1}{2}$ab=$\frac{1}{2}$c²+ab,
即$\frac{1}{2}$(a²+b²)+ab=$\frac{1}{2}$c²+ab,
∴a²+b²=c².
设梯形ACED的面积为S,则S=$\frac{1}{2}$(a+b)(a+b)=$\frac{1}{2}$(a²+b²)+ab,
又S=S△BDA+2S△ABC=$\frac{1}{2}$c²+2×$\frac{1}{2}$ab=$\frac{1}{2}$c²+ab,
即$\frac{1}{2}$(a²+b²)+ab=$\frac{1}{2}$c²+ab,
∴a²+b²=c².
查看更多完整答案,请扫码查看


