《2025年启东中学作业本八年级数学上册苏科版徐州专版》

1. 线段垂直平分线上的点到线段两端的距离相等；线段是轴对称图形,线段的垂直平分线是它的对称轴。

答案： 线段两端　轴对称　垂直平分线

2. 到线段两端距离相等的点在线段的垂直平分线上；线段的垂直平分线是到线段两端距离相等的点的集合。

答案： 垂直平分线　相等

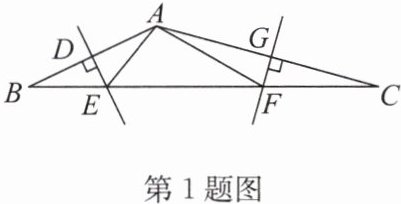
1. (锡山区月考)如图,在$\triangle ABC$中,$AB$,$AC的垂直平分线分别交BC于点E$,$F$。
(1)若$\triangle AEF的周长为10cm$,求$BC$的长；
(2)若$\angle BAC = 110^{\circ}$,求$\angle EAF$的度数。

答案： 1.解:
(1)
∵AB,AC的垂直平分线分别交BC于点E,F,
∴EA=EB,FA=FC.
∵△AEF的周长为10 cm,
∴AE+EF+AF=10 cm,
∴EB+EF+FC=10 cm,即BC=10 cm.
(2)
∵∠BAC=110°,
∴∠B+∠C=180°-∠BAC=70°.
∵EA=EB,FA=FC,
∴∠EAB=∠B,∠FAC=∠C,
∴∠EAB+∠FAC=∠B+∠C=70°,
∴∠EAF =∠BAC -∠EAB -∠FAC =110°-70°=40°.

2. 某镇准备新建一个医疗点$P$,使点$P到该镇所属A$村、$B$村、$C$村的距离都相等($A$村、$B$村、$C$村不在同一条直线上,地理位置如图所示)。请你用尺规作图的方法确定点$P$的位置。(不写作法,保留作图痕迹)

答案：
2.解:如答图，点P即为所求作.

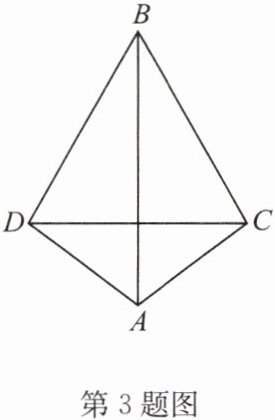
3. 如图,$BA平分\angle CBD$,$AB平分\angle CAD$。求证：$AB垂直平分CD$。

答案： 3.证明:
∵BA平分∠CBD,
∴∠DBA=∠CBA.
∵AB平分∠CAD,
∴∠DAB=∠CAB.
在△BAD和△BAC中,∠DBA=∠CBA,BA=BA,∠DAB=∠CAB,
∴△BAD≌△BAC(ASA),
∴BD=BC,AD=AC,
∴点B,A都在CD的垂直平分线上,
∴AB垂直平分CD.