《2025年启东中学作业本八年级数学上册苏科版徐州专版》

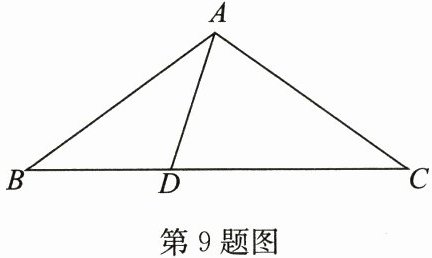
9. (10分)如图,在$\triangle ABC$中,$AB= AC= CD$,点$D在BC$上,且$AD= BD$.
(1)求证:$∠ADB= ∠BAC$;
(2)求$∠B$的度数.

答案：
(1)证明:
∵AB=AC,AD=BD,
∴∠B=∠C,∠B=∠BAD,
∴∠C=∠BAD.
∵∠ADB=∠DAC+∠C,∠BAC=∠BAD+∠DAC,
∴∠ADB=∠BAC;　
(2)解:
∵AC=CD,
∴∠DAC=∠ADC.　又
∵∠ADC=∠B+∠BAD=2∠B,
∴∠DAC=2∠B.　在△ABC中,∠B+∠BAC+∠C=5∠B=180°,
∴∠B=36°.

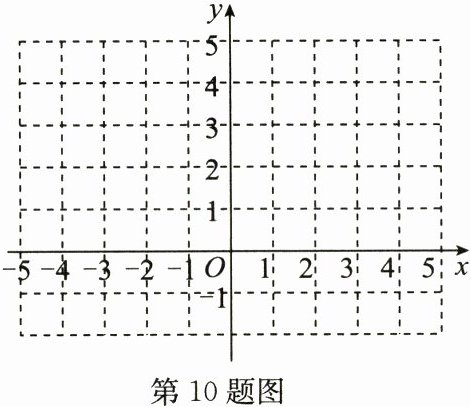
10. (15分)如图,在平面直角坐标系中,已知$A(0,1),B(2,0),C(4,3)$.
(1)在平面直角坐标系中画出$\triangle ABC$,并求$\triangle ABC$的面积;
(2)若点$D与点C关于y$轴对称,则点$D$的坐标为______;
(3)已知$P为x$轴上一点,若$\triangle ABP的面积为1$,求点$P$的坐标.

答案：

(1)解:如答图所示，△ABC为所求.　S△ABC=3×4−$\frac{1}{2}$×2×3−$\frac{1}{2}$×1×2−$\frac{1}{2}$×2×4=4.　　　　　 　
(2)(−4,3)　
(3)解:
∵P为x轴上一点，△ABP的面积为1,
∴BP=2.故点P的坐标为(4,0)或(0,0).

11. (15分)(南京一模)一辆货车和一辆轿车先后从甲地出发,沿一条笔直的公路匀速开往乙地.图中的线段$OA和线段BC分别表示货车和轿车离甲地的距离y(km)与货车出发时间x(h)$之间的函数关系.
(1)轿车出发时,两车相距84$km$;
(2)若轿车比货车提前$0.6h$到达乙地,求线段$BC对应的函数表达式及a$的值;
解:根据题意，得点C的坐标为(4.4,300).　设线段BC对应的函数表达式为y=kx+b,将C(4.4,300),B(1.4,0)代入,得{4.4k+b=300,1.4k+b=0,解得{k=100,b=-140.　∴线段BC对应的函数表达式为y=100x−140(1.4≤x≤4.4).　由图象可知，轿车在货车出发a h追上货车，则　100a−140=60a,解得a=3.5.
(3)若轿车出发$1.6h时与货车的距离小于12km$,直接写出轿车速度$v$的取值范围.105 km/h＜v＜120 km/h

答案：
(1)84 　
(2)解:根据题意，得点C的坐标为(4.4,300).　设线段BC对应的函数表达式为y=kx+b,将C(4.4,300),B(1.4,0)代入,得{4.4k+b=300,1.4k+b=0,解得{k=100,b=-140.
∴线段BC对应的函数表达式为y=100x−140(1.4≤x≤4.4).　由图象可知，轿车在货车出发a h追上货车，则　100a−140=60a,解得a=3.5.　
(3)105 km/h＜v＜120 km/h.

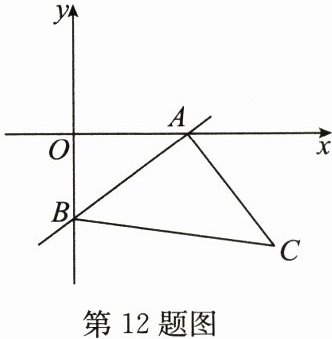
12. (20分)如图,一次函数$y= \frac {3}{4}x-3的图象分别与x$轴、$y轴交于点A,B$,以线段$AB为边在第四象限内作等腰直角三角形ABC$,且$∠BAC= 90^{\circ }$.
(1)写出点$A,B$的坐标;
(2)求点$C$的坐标;
(3)求直线$BC$的函数表达式.

答案：
解:
(1)点A的坐标为(4,0),点B的坐标为(0,−3).　
(2)
∵A(4,0),B(0,−3),
∴OA=4,OB=3.　如答图，过点C作CD⊥x轴，垂足为D.
∵∠BAC=90°,
∴∠OAB+∠DAC=90°,　又
∵CD⊥x轴,
∴∠DCA+∠DAC=90°,
∴∠ACD=∠OAB.
∵△ABC是等腰直角三角形，
∴AB=AC;　在△AOB和△CDA中,{∠BOA=∠ADC,∠OAB=∠DCA,AB=CA,
∴△AOB≌△CDA(AAS),
∴AD=OB=3,CD=OA=4,
∴OD=7,
∴点C的坐标为(7,−4).　　　　　　
(3)设直线BC的函数表达式为y=kx+b,把B(0,−3),C(7,−4)代入,得{b=-3,7k+b=-4,解得{k=-$\frac{1}{7}$,b=-3.
∴直线BC的函数表达式为y=−$\frac{1}{7}$x−3.