《2025年启东中学作业本八年级数学上册苏科版徐州专版》

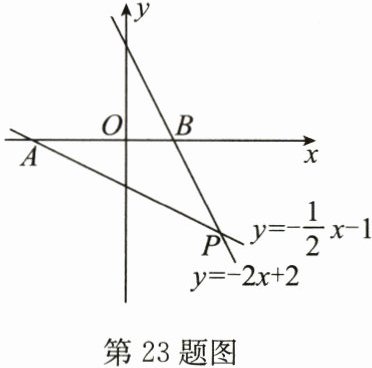
23.(15分)如图,在平面直角坐标系中,直线$y= -\frac {1}{2}x-1与直线y= -2x+2$相交于点P,并分别与x轴相交于点A,B.
(1)求交点P的坐标;
(2)求$\triangle PAB$的面积;
(3)请把图象中直线$y= -2x+2在直线y= -\frac {1}{2}x-1$上方的部分描黑加粗,并写出此时自变量x的取值范围.

答案：
解:
(1)联立$\left\{\begin{array}{l} y=-\frac{1}{2}x-1,\\ y=-2x+2,\end{array}\right.$解得$\left\{\begin{array}{l} x=2,\\ y=-2,\end{array}\right.$
∴点P的坐标为(2,-2).
(2)在y=-$\frac{1}{2}$x-1中,令y=0,则-$\frac{1}{2}$x-1=0,解得x=-2,
∴A(-2,0).在y=-2x+2中,令y=0,则-2x+2=0,解得x=1,
∴B(1,0),
∴AB=3,
∴$S_{\triangle PAB}$=$\frac{1}{2}$AB·|y_P|=$\frac{1}{2}$×3×2=3.
(3)如答图所示. 自变量x的取值范围是x＜2.