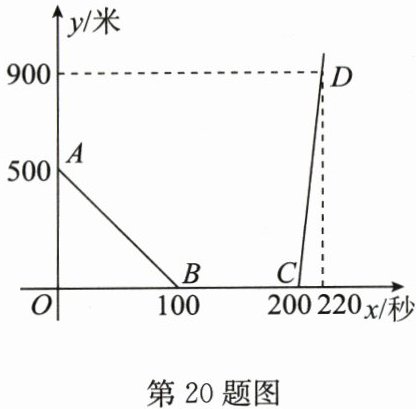
20.(8分)(2024秋·姜堰区期末)甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y米,y关于x的函数图象如图所示.
(1)求直线AB的函数表达式;
(2)求乙车的速度.
(1)求直线AB的函数表达式;
(2)求乙车的速度.

答案:
解:
(1)设直线AB的函数表达式为y=kx+b.
∵点(0,500),(100,0)在该函数图象上,
∴$\left\{\begin{array}{l} b=500,\\ 100k+b=0,\end{array}\right.$解得$\left\{\begin{array}{l} k=-5,\\ b=500.\end{array}\right.$即直线AB的函数表达式为y=-5x+500.
(2)设甲车的速度为m米/秒,乙车的速度为n米/秒,则$\left\{\begin{array}{l} 100n-100m=500,\\ (220-200)m+(220-200)n=900,\end{array}\right.$解得$\left\{\begin{array}{l} m=20,\\ n=25,\end{array}\right.$答:乙车的速度为25米/秒.
(1)设直线AB的函数表达式为y=kx+b.
∵点(0,500),(100,0)在该函数图象上,
∴$\left\{\begin{array}{l} b=500,\\ 100k+b=0,\end{array}\right.$解得$\left\{\begin{array}{l} k=-5,\\ b=500.\end{array}\right.$即直线AB的函数表达式为y=-5x+500.
(2)设甲车的速度为m米/秒,乙车的速度为n米/秒,则$\left\{\begin{array}{l} 100n-100m=500,\\ (220-200)m+(220-200)n=900,\end{array}\right.$解得$\left\{\begin{array}{l} m=20,\\ n=25,\end{array}\right.$答:乙车的速度为25米/秒.
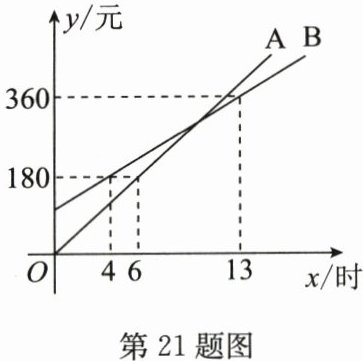
21.(10分)某游泳馆推出了A,B两种季度套餐,选择这两种套餐消费时,一个季度的费用y(元)与该季度游泳时长x(时)之间的函数关系如图所示.
(1)分别求出这两种套餐消费时,y与x之间的函数表达式;
(2)请通过计算说明,一个季度的游泳时长少于多少时选择A套餐更省钱;
(3)小明估计了自己本季度的游泳时长后,选择了B套餐,因为这样可比选择A套餐游泳平均每小时节省5元,求小明估计自己本季度的游泳时长.
(1)分别求出这两种套餐消费时,y与x之间的函数表达式;
(2)请通过计算说明,一个季度的游泳时长少于多少时选择A套餐更省钱;
(3)小明估计了自己本季度的游泳时长后,选择了B套餐,因为这样可比选择A套餐游泳平均每小时节省5元,求小明估计自己本季度的游泳时长.

答案:
解:
(1)设$y_A$=$k_1$x.根据题意,得6$k_1$=180,解得$k_1$=30,
∴$y_A$=30x.设$y_B$=$k_2$x+b,根据题意,得$\left\{\begin{array}{l} 4k_2+b=180,\\ 13k_2+b=360\end{array}\right.$解得$\left\{\begin{array}{l} k_2=20,\\ b=100.\end{array}\right.$
∴$y_B$=20x+100.
(2)由题意,得30x<20x+100,解得x<10.答:一个季度的游泳时长少于10小时时选择A套餐更省钱.
(3)由题意,得30x-(20x+100)=5x,解得x=20.答:小明估计自己本季度的游泳时长为20小时.
(1)设$y_A$=$k_1$x.根据题意,得6$k_1$=180,解得$k_1$=30,
∴$y_A$=30x.设$y_B$=$k_2$x+b,根据题意,得$\left\{\begin{array}{l} 4k_2+b=180,\\ 13k_2+b=360\end{array}\right.$解得$\left\{\begin{array}{l} k_2=20,\\ b=100.\end{array}\right.$
∴$y_B$=20x+100.
(2)由题意,得30x<20x+100,解得x<10.答:一个季度的游泳时长少于10小时时选择A套餐更省钱.
(3)由题意,得30x-(20x+100)=5x,解得x=20.答:小明估计自己本季度的游泳时长为20小时.
查看更多完整答案,请扫码查看


