10. (14分) 如图, 在四边形 $ ABCD $ 中, $ \angle ABC = \angle ADC = 90^{\circ} $, $ E $ 是 $ AC $ 的中点, 连接 $ BE, BD, DE $.
(1) 求证: $ \triangle BED $ 是等腰三角形;
(2) 当 $ \angle BAD $ 的度数为

(1)证明:$\because\angle ABC=90^{\circ}$,E是AC的中点,
$\therefore BE=\frac{1}{2}AC$.
同理可得,$DE=\frac{1}{2}AC$,$\therefore BE=DE$,
$\therefore\triangle BED$是等腰三角形.
(1) 求证: $ \triangle BED $ 是等腰三角形;
(2) 当 $ \angle BAD $ 的度数为
$30^{\circ}$
时, $ \triangle BED $ 是等边三角形.
(1)证明:$\because\angle ABC=90^{\circ}$,E是AC的中点,
$\therefore BE=\frac{1}{2}AC$.
同理可得,$DE=\frac{1}{2}AC$,$\therefore BE=DE$,
$\therefore\triangle BED$是等腰三角形.
答案:
(1)证明:$\because\angle ABC=90^{\circ}$,E是AC的中点,
$\therefore BE=\frac{1}{2}AC$.
同理可得,$DE=\frac{1}{2}AC$,$\therefore BE=DE$,
$\therefore\triangle BED$是等腰三角形.
(2)$30^{\circ}$
(1)证明:$\because\angle ABC=90^{\circ}$,E是AC的中点,
$\therefore BE=\frac{1}{2}AC$.
同理可得,$DE=\frac{1}{2}AC$,$\therefore BE=DE$,
$\therefore\triangle BED$是等腰三角形.
(2)$30^{\circ}$
11. (16分) 已知学生公寓、阅览室、超市依次在同一条直线上, 阅览室离学生公寓 $ 1.2 \, \text{km} $, 超市离学生公寓 $ 2 \, \text{km} $. 小明从学生公寓出发, 匀速步行了 $ 12 \, \text{min} $ 到阅览室; 在阅览室停留 $ 70 \, \text{min} $ 后, 匀速步行了 $ 10 \, \text{min} $ 到超市; 在超市停留 $ 20 \, \text{min} $ 后, 匀速骑行了 $ 8 \, \text{min} $ 返回学生公寓. 如图所示的图象反映了这个过程中小明离学生公寓的距离 $ y(\text{km}) $ 与离开学生公寓的时间 $ x(\text{min}) $ 之间的关系. 请根据相关信息, 解答下列问题:
(1) 填表:
| 离开学生公寓的时间/min | 5 | 8 | 50 | 87 | 112 |
| 离学生公寓的距离/km | 0.5 |
(2) 回公寓的路上, 小明何时距公寓 $ 0.5 \, \text{km} $?

解:小明回公寓时的速度为$\frac{2}{120 - 112}=\frac{1}{4}(\text{km/min})$,
$\therefore$小明走0.5 km所需要的时间为$\frac{0.5}{\frac{1}{4}} = 2(\text{min})$,
120 - 2 = 118(min).
答:小明在离开公寓118 min时距公寓0.5 km.
(1) 填表:
| 离开学生公寓的时间/min | 5 | 8 | 50 | 87 | 112 |
| 离学生公寓的距离/km | 0.5 |
0.8
| 1.2
| 1.6
| 2 |(2) 回公寓的路上, 小明何时距公寓 $ 0.5 \, \text{km} $?

解:小明回公寓时的速度为$\frac{2}{120 - 112}=\frac{1}{4}(\text{km/min})$,
$\therefore$小明走0.5 km所需要的时间为$\frac{0.5}{\frac{1}{4}} = 2(\text{min})$,
120 - 2 = 118(min).
答:小明在离开公寓118 min时距公寓0.5 km.
答案:
(1)0.8 1.2 1.6
(2)解:小明回公寓时的速度为$\frac{2}{120 - 112}=\frac{1}{4}(\text{km/min})$,
$\therefore$小明走0.5 km所需要的时间为$\frac{0.5}{\frac{1}{4}} = 2(\text{min})$,
120 - 2 = 118(min).
答:小明在离开公寓118 min时距公寓0.5 km.
(1)0.8 1.2 1.6
(2)解:小明回公寓时的速度为$\frac{2}{120 - 112}=\frac{1}{4}(\text{km/min})$,
$\therefore$小明走0.5 km所需要的时间为$\frac{0.5}{\frac{1}{4}} = 2(\text{min})$,
120 - 2 = 118(min).
答:小明在离开公寓118 min时距公寓0.5 km.
12. (18分) 【数学概念】过三角形边上的一点作两条直线, 分别与三角形另外两边相交, 若截得的两个三角形全等, 则称该点为三角形的全等点.
【理解运用】在 $ \triangle ABC $ 中, $ D $ 是边 $ BC $ 上的点, 过点 $ D $ 的两条直线 $ DE, DF $ 与边 $ AB, AC $ 分别交于点 $ E, F $.
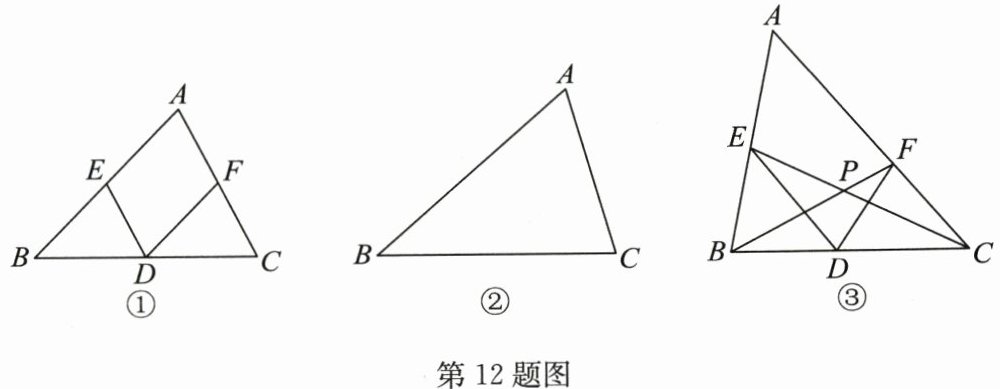
(1) 如图①, 若 $ D $ 是 $ BC $ 的中点, 且 $ DE // AC $, $ DF // AB $. 求证: $ D $ 是 $ \triangle ABC $ 的全等点;
(2) 如图②, 已知 $ \triangle ABC $, 用直尺和圆规在边 $ BC $ 上作出点 $ D $, 使 $ D $ 是 $ \triangle ABC $ 的全等点, 且 $ DE // AC $, $ DF $ 与 $ AB $ 不平行; (保留作图痕迹, 写出必要的文字说明)
(3) 如图③, $ D $ 是 $ \triangle ABC $ 的全等点, 且 $ AB < AC $, $ DE $ 与 $ AC $ 不平行, $ DF $ 与 $ AB $ 不平行, $ BF $ 与 $ CE $ 交于点 $ P $, 请探索 $ \angle A $ 与 $ \angle PBC $ 之间的数量关系, 并说明理由.
【理解运用】在 $ \triangle ABC $ 中, $ D $ 是边 $ BC $ 上的点, 过点 $ D $ 的两条直线 $ DE, DF $ 与边 $ AB, AC $ 分别交于点 $ E, F $.
(1) 如图①, 若 $ D $ 是 $ BC $ 的中点, 且 $ DE // AC $, $ DF // AB $. 求证: $ D $ 是 $ \triangle ABC $ 的全等点;
(2) 如图②, 已知 $ \triangle ABC $, 用直尺和圆规在边 $ BC $ 上作出点 $ D $, 使 $ D $ 是 $ \triangle ABC $ 的全等点, 且 $ DE // AC $, $ DF $ 与 $ AB $ 不平行; (保留作图痕迹, 写出必要的文字说明)
(3) 如图③, $ D $ 是 $ \triangle ABC $ 的全等点, 且 $ AB < AC $, $ DE $ 与 $ AC $ 不平行, $ DF $ 与 $ AB $ 不平行, $ BF $ 与 $ CE $ 交于点 $ P $, 请探索 $ \angle A $ 与 $ \angle PBC $ 之间的数量关系, 并说明理由.

答案:
(1)证明:$\because$D是BC的中点,$\therefore BD=CD$.
$\because DE// AC$,$DF// AB$,$\therefore\angle EDB=\angle C$,$\angle CDF=\angle B$,
$\therefore\triangle BDE\cong\triangle DCF(\text{ASA})$,$\therefore$D是$\triangle ABC$的全等点.
(2)解:如答图,作$\angle ACB$的平分线交AB于点E,作$ED// AC$,交BC于点D.在AC上截取$CF=BD$.连接DF,则点D是$\triangle ABC$的全等点.理由如下:

$\because$CE平分$\angle ACB$,$\therefore\angle ACE=\angle BCE$.
$\because DE// AC$,$\therefore\angle BDE=\angle FCD$,$\angle DEC=\angle ACE=\angle DCE$,$\therefore DE=CD$.又$BD=FC$,
$\therefore\triangle BDE\cong\triangle FCD(\text{SAS})$,$\therefore$D是$\triangle ABC$的全等点.
(3)解:$\angle A=2\angle PBC$.理由如下:
$\because AB<AC$,DE与AC不平行,DF与AB不平行,
$\therefore\angle ABC\neq\angle ACB$,$\angle ACB\neq\angle BDE$,$\angle ABC\neq\angle FDC$.
$\because$D是$\triangle ABC$的全等点,$\therefore\triangle BDE\cong\triangle FDC$,
$\therefore BD=DF$,$DE=DC$,$\angle EBD=\angle CFD$.
$\therefore\angle DBF=\angle DFB$.
$\because\angle DFC+\angle AFD=180^{\circ}$,$\therefore\angle DBE+\angle AFD=180^{\circ}$.
$\because$四边形ABDF的内角和为$360^{\circ}$,
$\therefore\angle A+\angle BDF=180^{\circ}$.
$\because\angle PBC+\angle DFB+\angle BDF=180^{\circ}$,
$\therefore\angle A=2\angle PBC$.
(1)证明:$\because$D是BC的中点,$\therefore BD=CD$.
$\because DE// AC$,$DF// AB$,$\therefore\angle EDB=\angle C$,$\angle CDF=\angle B$,
$\therefore\triangle BDE\cong\triangle DCF(\text{ASA})$,$\therefore$D是$\triangle ABC$的全等点.
(2)解:如答图,作$\angle ACB$的平分线交AB于点E,作$ED// AC$,交BC于点D.在AC上截取$CF=BD$.连接DF,则点D是$\triangle ABC$的全等点.理由如下:

$\because$CE平分$\angle ACB$,$\therefore\angle ACE=\angle BCE$.
$\because DE// AC$,$\therefore\angle BDE=\angle FCD$,$\angle DEC=\angle ACE=\angle DCE$,$\therefore DE=CD$.又$BD=FC$,
$\therefore\triangle BDE\cong\triangle FCD(\text{SAS})$,$\therefore$D是$\triangle ABC$的全等点.
(3)解:$\angle A=2\angle PBC$.理由如下:
$\because AB<AC$,DE与AC不平行,DF与AB不平行,
$\therefore\angle ABC\neq\angle ACB$,$\angle ACB\neq\angle BDE$,$\angle ABC\neq\angle FDC$.
$\because$D是$\triangle ABC$的全等点,$\therefore\triangle BDE\cong\triangle FDC$,
$\therefore BD=DF$,$DE=DC$,$\angle EBD=\angle CFD$.
$\therefore\angle DBF=\angle DFB$.
$\because\angle DFC+\angle AFD=180^{\circ}$,$\therefore\angle DBE+\angle AFD=180^{\circ}$.
$\because$四边形ABDF的内角和为$360^{\circ}$,
$\therefore\angle A+\angle BDF=180^{\circ}$.
$\because\angle PBC+\angle DFB+\angle BDF=180^{\circ}$,
$\therefore\angle A=2\angle PBC$.
查看更多完整答案,请扫码查看


