《2025年启东中学作业本八年级数学上册苏科版徐州专版》

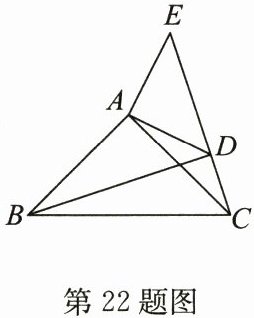
22.(12分)如图,在$△ABC$,$△ADE$中,$∠BAC= ∠DAE= 90^{\circ }$,$AB= AC$,$AD= AE$,C,D,E三点在同一条直线上,连接BD,则CE,BD有怎样的数量关系和位置关系? 证明你的结论.

答案： 解:CE=BD且CE⊥BD.证明如下:
∵∠BAC=∠DAE=90°,∠BAD=∠BAC+∠CAD,∠CAE=∠CAD+∠DAE,
∴∠BAD=∠CAE.
在△BAD和△CAE中,$\left\{\begin{array}{l} BA=CA,\\ ∠BAD=∠CAE,\\ AD=AE,\end{array}\right. $
∴△BAD≌△CAE(SAS),
∴BD=CE,∠ABD=∠ACE.
∵∠ABC+∠ACB=90°,∠ABC=∠ABD+∠DBC,
∴∠ACE+∠DBC+∠ACB=90°,
∴∠BDC=90°,
∴BD⊥CE.

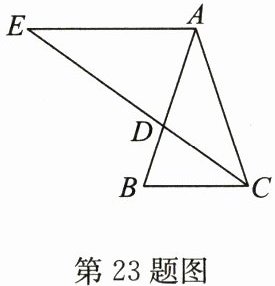
23.(12分)如图,在$△ABC$中,$AB= AC$,$∠BAC= 36^{\circ }$,CD是$∠ACB$的平分线,CD交AB于点D,过点A作$AE// BC$,交CD的延长线于点E.
(1)求$∠ADC$的度数;
(2)求证:$AE= AC$;
(3)$△ADE$是等腰三角形吗? 请说明理由.

答案：
(1)解:
∵AB=AC,∠BAC=36°,
∴∠B=∠ACB=$\frac{1}{2}$(180°−∠BAC)=72°.
∵CD是∠ACB的平分线，
∴∠DCB=$\frac{1}{2}$∠ACB=$\frac{1}{2}$×72°=36°,
∴∠ADC=∠B+∠DCB=72°+36°=108°.
(2)证明:
∵CD是∠ACB的平分线，
∴∠BCE=∠ACE.
∵AE//BC,
∴∠BCE=∠E,
∴∠ACE=∠E,
∴AE=AC.
(3)解:△ADE是等腰三角形.理由如下:
∵AE//BC,
∴∠EAB=∠B=72°.
∵∠B=72°,∠DCB=36°,
∴∠ADE=∠BDC=180°−72°−36°=72°,
∴∠EAD=∠ADE,
∴AE=DE,
∴△ADE是等腰三角形.

24.(18分)如图,$△ABC$是等边三角形,点C关于AB的对称点为点$C'$,P是直线$C'B$上的一个动点.
(1)若P是线段$C'B$上任意一点(不与点$C'$,B重合).
①如图①,作$∠PAE= 60^{\circ }$交BC于点E,AP与AE相等吗? 请证明你的结论;
②如图②,连接AP,作$∠APD= 60^{\circ }$交射线BC于点D,PD与PA相等吗? 请证明你的结论.
(2)若点P在线段$C'B$的延长线上.
①连接AP,作$∠APD= 60^{\circ }$交射线BC于点D,依题意在图③中补全图形;
②请写出线段BD,AB,BP之间的数量关系,并说明理由.

答案：
解:
(1)①AP=AE.证明如下:
∵△ABC是等边三角形，
∴∠ABC=∠BAC=60°,AB=AC.
∵点C'与点C关于AB对称,
∴∠C'BA=∠CBA=60°.
∵∠PAE=∠BAC=60°,
∴∠PAB=∠EAC,
∴△PAB≌△EAC(ASA),
∴AP=AE.
　②PD=PA.证明如下:
　如答图①,作∠BPE=60°交AB于点E.
∵△ABC是等边三角形,
∴∠ABC=60°.
∵点C'与点C关于AB对称，
∴∠C'BA=∠CBA=60°=∠BPE,
∴∠PEB=60°,
∴△PBE是等边三角形，
∴PB=PE,∠AEP=∠PBD=120°.
∵∠BPD+∠DPE=60°,∠APE+∠DPE=60°,
∴∠BPD=∠EPA.
在△PBD和△PEA中,$\left\{\begin{array}{l} ∠BPD=∠EPA,\\ PB=PE,\\ ∠PBD=∠PEA,\end{array}\right. $
∴△PBD≌△PEA(ASA),
∴PD=PA.
　　　
(2)①补全图形如答图②所示.
　②BD=BP+AB.理由如下:
　如答图②,在BD上取一点E,使得BE=PB,
∵∠EBP=60°,BE=BP,
∴△EBP是等边三角形，
∴∠BEP=∠BPE=∠APD=60°,
∴∠PED=∠ABP=120°,∠APB=∠DPE.
　又
∵PB=PE,
∴△BPA≌△EPD(ASA),
∴AB=DE,
∴BD=BE+ED=BP+AB.