1. 已知一次函数$y= kx+b$中,函数值$y随自变量x$的增大而减小,且$kb<0$,则函数$y= kx+b$的图象大致是 (

C
)
答案:
C
2. 如图,在$\triangle ABC$中,$∠BAC= 90^{\circ },AB= AC$,点$D在BC$上,且$BD= BA$,则$∠CAD$的度数为 (
A.$30^{\circ }$
B.$25^{\circ }$
C.$22.5^{\circ }$
D.$21^{\circ }$
C
)A.$30^{\circ }$
B.$25^{\circ }$
C.$22.5^{\circ }$
D.$21^{\circ }$
答案:
C
3. 在$Rt\triangle ABC$中,$∠C= 90^{\circ },BC= n^{2}-1,AB= n^{2}+1$,则$AC$的长为 (
A.$2n$
B.$2n^{2}$
C.$4n$
D.$4n^{2}$
A
)A.$2n$
B.$2n^{2}$
C.$4n$
D.$4n^{2}$
答案:
A
4. 如图①,在正方形$ABCD的边BC上有一点E$,连接$AE$.点$P从正方形的顶点A$出发,沿$A→D→C以1cm/s的速度匀速运动到点C$.图②是点$P$运动时,$\triangle APE的面积y(cm^{2})随时间x(s)$变化的函数图象.当$x= 6$时,$y$的值为 (
A.$6$
B.$7$
C.$\frac {13}{2}$
D.$\frac {11}{2}$
B
)A.$6$
B.$7$
C.$\frac {13}{2}$
D.$\frac {11}{2}$
答案:
B
5. 点$Q(1,4)$到x轴的距离是
4
.
答案:
4
6. 一次函数$y_{1}= kx+b与y_{2}= mx+n$的部分自变量和对应函数值如下表:
| $x$ | …$$ | $-2$ | $-1$ | $0$ | $1$ | $2$ | …$$ |
| $y_{1}$ | …$$ | $5$ | $2$ | $-1$ | $-4$ | $-7$ | …$$ |
| $y_{2}$ | …$$ | $1$ | $2$ | $3$ | $4$ | $5$ | …$$ |
则关于$x的不等式kx+b>mx+n$的解集是______
| $x$ | …$$ | $-2$ | $-1$ | $0$ | $1$ | $2$ | …$$ |
| $y_{1}$ | …$$ | $5$ | $2$ | $-1$ | $-4$ | $-7$ | …$$ |
| $y_{2}$ | …$$ | $1$ | $2$ | $3$ | $4$ | $5$ | …$$ |
则关于$x的不等式kx+b>mx+n$的解集是______
x<−1
.
答案:
x<−1
7. (无锡期末)如图,长为$2.5m$的梯子靠在墙上,梯子的底端离墙脚线的距离为$1.5m$,则梯子顶端的高度$h$是
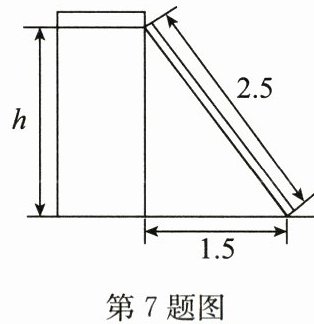
2
$m$.
答案:
2
8. “三等分角”是由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒$OA,OB$组成,两根棒在$O点相连并可绕O$转动,$C$点固定,$OC= CD= DE$,点$D,E$可在槽中滑动.若$∠BDE= 75^{\circ }$,则$∠CDE$的度数是______
80°
.
答案:
80°
查看更多完整答案,请扫码查看


