第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
11. (教材复习题第 11 题改编)下列有关绝对值的说法:①有理数的绝对值一定不是负数;②如果两个数不相等,那么这两个数的绝对值也不相等;③负数的绝对值一定是它的相反数;④绝对值等于它本身的数一定是正数。其中正确的有
①③
。(填序号)
答案:
①③
12. 若 $ |4 - a| + |2 - b| = 0 $,则 ab 的结果为
8
。
答案:
8 [解析]因为|4-a|+|2-b|=0,所以4-a=0,2 -b=0,所以a=4,b=2,所以ab=4×2=8.
13. 传统文化情境 中国建筑 如图,广济桥是中国四大古桥之一,全长 518 米。小明测量了 5 次桥长,测得的数据(单位:米)分别是:518.4,517.8,518.2,517.9,517.7。如果以 518 米为标准,超过标准长度的部分记为正,不足标准长度的部分记为负。
(1)试用正、负数在下表中表示出小明测得的数据:
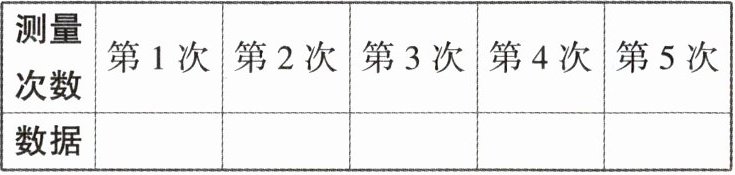
(2)请问哪次测得的结果最接近实际桥长?并说明理由。

(1)试用正、负数在下表中表示出小明测得的数据:

测量次数 第1次第2次第3次第4次第5次
数据 +0.4 -0.2 +0.2 -0.1 -0.3
数据 +0.4 -0.2 +0.2 -0.1 -0.3
(2)请问哪次测得的结果最接近实际桥长?并说明理由。

第4次测得的结果最接近实际桥长。理由如下:因为|+0.4|=0.4,|-0.2|=0.2,|+0.2|=0.2,|-0.1|=0.1,|-0.3|=0.3,0.4>0.3>0.2>0.1,所以第4次测得的结果最接近实际桥长。
答案:
解:
(1)填表如下:
测量次数 第1次第2次第3次第4次第5次
数据 +0.4 -0.2 +0.2 -0.1 -0.3
答案详解详析
(2)第4次测得的结果最接近实际桥长.理由
如下:
因为|+0.4|=0.4,|-0.2|=0.2,|+0.2|=0.2,
|-0.1|=0.1,|-0.3|=0.3,
0.4>0.3>0.2>0.1,
所以第4次测得的结果最接近实际桥长.
(1)填表如下:
测量次数 第1次第2次第3次第4次第5次
数据 +0.4 -0.2 +0.2 -0.1 -0.3
答案详解详析
(2)第4次测得的结果最接近实际桥长.理由
如下:
因为|+0.4|=0.4,|-0.2|=0.2,|+0.2|=0.2,
|-0.1|=0.1,|-0.3|=0.3,
0.4>0.3>0.2>0.1,
所以第4次测得的结果最接近实际桥长.
14. (中考新考法·阅读理解题)我们知道 $ |x| $表示 x 在数轴上对应的点到原点的距离,$ |x - a| $表示数 x 与 a 在数轴上对应的点之间的距离。例:$ |x - 1| = 2 $表示数 x 与 1 在数轴上表示的点的距离是 2 个单位长度,如图所示,即可得出 x 的值为 -1 或 3。
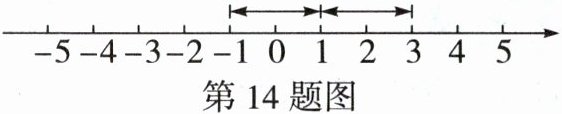
根据以上材料,解答下列问题:
(1)若 $ |x - 2| = 4 $,则 x 的值为______;
(2)若数轴上表示数 a 的点位于表示 -3 与 2 的两点之间,则 $ |a + 3| + |a - 2| $的值是多少?
(3)已知有理数 b,则 $ |b + 5| + |b - 3| $的计算结果是否有最小值?若有,请求出最小值;若没有,请说出理由。
[此考法江苏、甘肃等地中考已考查]
视频讲解
中考新考法题

根据以上材料,解答下列问题:
(1)若 $ |x - 2| = 4 $,则 x 的值为______;
(2)若数轴上表示数 a 的点位于表示 -3 与 2 的两点之间,则 $ |a + 3| + |a - 2| $的值是多少?
(3)已知有理数 b,则 $ |b + 5| + |b - 3| $的计算结果是否有最小值?若有,请求出最小值;若没有,请说出理由。
[此考法江苏、甘肃等地中考已考查]
视频讲解
中考新考法题
答案:
解:
(1)-2或6; [解法提示]如解图①,在数轴
上与2对应的点的距离为4个单位长度的点表
示的数为-2或6.

(2)|a+3|+|a-2|表示在数轴上表示数a的点到
表示-3与2的点的距离之和,
因为表示数a的点位于表示-3与2的两点之间,
如解图②,所以无论表示数a的点在表示-3与2
的两点之间的什么位置,表示数a的点到表示
-3与2的点的距离之和,始终为表示-3的点到
表示2的点的距离,
即|a+3|+|a-2|的计算结果为5;

(3)|b+5|+|b-3|的计算结果有最小值,因为|b+5|+|b-3|表示在数轴上表示数b的点到
表示-5与3的点的距离之和,
所以当b=-5或-5<b<3或b=3时,这个距离之和最小,
最小值就是表示-5与3的两点之间的距离,为8个单位长度,
所以|b+5|+|b-3|的计算结果有最小值为8.
解:
(1)-2或6; [解法提示]如解图①,在数轴
上与2对应的点的距离为4个单位长度的点表
示的数为-2或6.

(2)|a+3|+|a-2|表示在数轴上表示数a的点到
表示-3与2的点的距离之和,
因为表示数a的点位于表示-3与2的两点之间,
如解图②,所以无论表示数a的点在表示-3与2
的两点之间的什么位置,表示数a的点到表示
-3与2的点的距离之和,始终为表示-3的点到
表示2的点的距离,
即|a+3|+|a-2|的计算结果为5;

(3)|b+5|+|b-3|的计算结果有最小值,因为|b+5|+|b-3|表示在数轴上表示数b的点到
表示-5与3的点的距离之和,
所以当b=-5或-5<b<3或b=3时,这个距离之和最小,
最小值就是表示-5与3的两点之间的距离,为8个单位长度,
所以|b+5|+|b-3|的计算结果有最小值为8.
1. 已知有理数 $ a $,$ b $ 满足 $ |a - 3| $ 与 $ |5 - b| $ 互为相反数,则 $ b - a $ 的计算结果为 (
A.$-2$
B.$2$
C.$3$
D.$5$
B
)A.$-2$
B.$2$
C.$3$
D.$5$
答案:
B
2. 已知 $ |a - b| + |b - c| + |c - d| = 0 $,则 $ a - b + c - d $ 的值为
0
.
答案:
0 【解析】因为|a-b|+|b-c|+|c-d|=0,所以a-b=0,b-c=0,c-d=0,所以a=b,b=c,c=d,所以a=b=c=d,所以a-b+c-d=0.
查看更多完整答案,请扫码查看


