《2025年万唯中考情境题七年级数学上册人教版》

8. 要使算式$(-5)○□2$的运算结果最小,则“○”“□”内应填入的分别是（B）
A.2,+
B.3,-
C.2,×
D.3,÷

答案： B

9. 定义一种新的运算:$a※b=a^2÷(b-1)$,例如$3※5=3^2÷(5-1)=9÷4=\frac{9}{4}$,则$(-3)※4$的结果为3.

答案： 3

10. (教材练习第 3 题改编)计算:
(1)$-3^2-(-0.75)×\frac{1}{3}-6÷|\frac{2}{3}-1|^2$；
(2)$-1^{12}-(0-1)×\frac{1}{3}×[2-(-3)^2]$；
(3)$(-4)^2-(1\frac{1}{2})^3×\frac{2}{9}-6÷|-\frac{2}{3}|^3$.

答案：
(1)解:原式=-9+$\frac{3}{4}$×$\frac{1}{3}$-6÷($\frac{1}{3}$)$^{2}$=-9+$\frac{1}{4}$-6×9=-9+0.25-54=-62.75；
(2)解:原式=-1-(0-1)×$\frac{1}{3}$×(2-9)=-1-(-1)×$\frac{1}{3}$×(-7)=-1-$\frac{7}{3}$=-$\frac{10}{3}$；
(3)解:原式=16-$\frac{27}{8}$×$\frac{2}{9}$-6÷$\frac{8}{27}$=16-$\frac{3}{4}$-$\frac{81}{4}$=-5

11. 已知$a^2=9$,$b$的倒数是$\frac{1}{2}$,$c$与 3 互为相反数,且$ab＜0$,求$ab-ac+bc$的值.

答案： 解:根据题意可得,a=-3,b=2,c=-3,所以ab-ac+bc=(-3)×2-(-3)×(-3)+2×(-3)=-6-9-6=-21

12. 跨学科情境 生物植物繁殖 水葫芦是一种水生漂浮植物,若在适宜的条件下,1 株水葫芦每 5 天就能繁殖 1 株(不考虑死亡、被打捞等其他因素).
(1)假设湖面上现有 1 株水葫芦,填写下表:
| 天数/天 | 5 | 10 | 15 | … | 50 |
|---------|-----|-----|-----|----|-----|
| 总株数/株 | 2 | 4 | 8 | … | 2¹⁰(或1024) |
(2)已知某流域的水葫芦数量维持在 700 株以内对水质净化有益,现有 10 株水葫芦,请通过计算说明一个月(按 30 天算)后该流域的水葫芦数量对水质净化是否有益.
解:因为30÷5=6,所以一个月后该区域水葫芦的数量为10×2⁶=640(株).因为640＜700,所以一个月后该流域的水葫芦数量对水质净化有益

答案：
(1)8,2$^{10}$(或1024)；
(2)解:因为30÷5=6,所以一个月后该区域水葫芦的数量为10×2$^{6}$=640(株).因为640＜700,所以一个月后该流域的水葫芦数量对水质净化有益

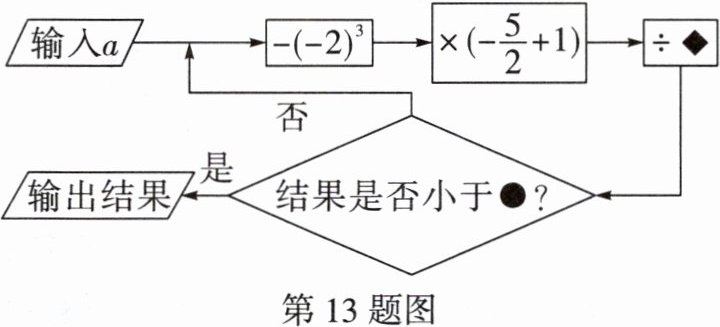
13. (中考新考法·选择条件开放)如图是一个有理数混合运算的流程图.例:当◆的值为 3,●的值为-1,输入$a$的值为 2 时,根据流程图可列式为$[2-(-2)^3]×(-\frac{5}{2}+1)÷3=-5$,$-5＜-1$,符合输出条件,输出结果为-5. 依照此流程,请你从-4,-2,6,12 这四个数中任选两个填入图中的“◆”“●”处,已知输入$a$的值为 8,求最终输出的结果.

答案： 解:选择将-4填入“◆”,6填入“●”.根据题意,输入a=8,可列式为:[8-(-2)$^{3}$]×(-$\frac{5}{2}$+1)÷(-4)=16×(-$\frac{3}{2}$)÷(-4)=6,6=6,不符合输出条件;所以输入a=6,[6-(-2)$^{3}$]×(-$\frac{5}{2}$+1)÷(-4)=14×(-$\frac{3}{2}$)÷(-4)=$\frac{21}{4}$,$\frac{21}{4}$＜6,符合输出条件,输出结果$\frac{21}{4}$.答:选择将-4填入“◆”,6填入“●”,输出结果为$\frac{21}{4}$.(答案不唯一)