《2025年万唯中考情境题七年级数学上册人教版》

9. 若多项式$2t-7与多项式-3(t-4)$的值互为相反数,则t的值为5.

答案： 5

10. 若方程$ax^{|a-2|-1}-1= 0$是关于x的一元一次方程,则a的值为4.

答案： 4 【解析】因为方程a^{|a-2|-1}-1=0是关于x的一元一次方程,所以|a-2|-1=1,移项,得|a-2|=2,当a-2＞0,则a-2=2,解得a=4.经检验,符合题意;当a-2＜0,则-(a-2)=2,解得a=0,经检验,不符合题意.所以a=4.

11. (教材习题第2题改编)解方程:$4(x-2)-7(3x-1)= 12(1-2x).$

答案： 解:去括号,得4x-8-21x+7=12-24x.
移项、合并同类项,得7x=13.
系数化为1,得$x=\dfrac{13}{7}.$

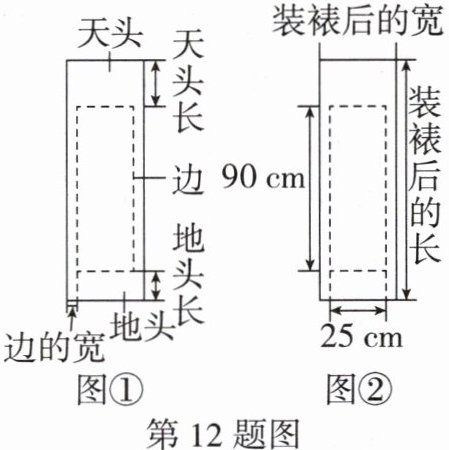
12. (黑白卷改编)如图①,对联装裱后上、下空白处分别称为天头和地头,左、右空白处统称为边.一般情况下,天头长与地头长的比是$6:4$,左、右边的宽相等,均为天头长与地头长的和的$\frac {1}{10}$.如图②,倩倩要装裱一副对联,对联的长为90cm,宽为25cm.若要求装裱后的长是装裱后的宽的4倍,求边的宽和天头长.

答案： 解:因为天头长与地头长的比是6:4,且左、右边的宽相等,均为天头长与地头长的和的$\dfrac{1}{10},$所以设天头长为6x cm,地头长为4x cm,则左、右边的宽为$\dfrac{6x+4x}{10}=x cm.$根据题意得,90+(6x+4x)=4×(25+2x).
去括号,得90+6x+4x=100+8x.
移项、合并同类项,得2x=10.
系数化为1,得x=5,6x=6×5=30(cm).
所以边的宽为5 cm,天头长为30 cm.

13. (中考新考法·解题策略开放)下面是方程$3(x+2)-(x+2)= 6$的两种解法:

(1)解法一中第①步的依据是去括号法则,解法二用到的数学思想是整体思想;
(2)选择一种你喜欢的解法解方程$5(x+3)+4= 20-3(x+3).$
选择解法一:
去括号,得5x+15+4=20-3x-9.
移项,得5x+3x=20-9-15-4.
合并同类项,得8x=-8.
两边同时除以8,得x=-1.
选择解法二:
移项,得5(x+3)+3(x+3)=20-4.
合并同类项,得8(x+3)=16.
两边同时除以8,得x+3=2.
两边同时减去3,得x=-1.(任选一种解法作答即可)

答案：
(1)去括号法则;整体思想;
(2)选择解法一:
去括号,得5x+15+4=20-3x-9.
移项,得5x+3x=20-9-15-4.
合并同类项,得8x=-8.
两边同时除以8,得x=-1.
选择解法二:
移项,得5(x+3)+3(x+3)=20-4.
合并同类项,得8(x+3)=16.
两边同时除以8,得x+3=2.
两边同时减去3,得x=-1.(任选一种解法作答即可)

1. 解方程：(1)$|3x - 5| = 10$； (2)$2|4x - 9| - 6 = 0$。

答案： 1. 解:
(1)当3x-5＞0,则3x-5=10,
解得x=5;
当3x-5＜0,则-(3x-5)=10,
解得$x=-\dfrac{5}{3}.$
所以方程的解为x=5或$x=-\dfrac{5}{3};$
(2)移项,得2|4x-9|=6.
方程两边同时除以2,得|4x-9|=3.
当4x-9＞0,则4x-9=3,
解得x=3;
当4x-9＜0,则4x-9=-3,
解得$x=\dfrac{3}{2}.$
所以方程的解为x=3或$x=\dfrac{3}{2}.$