第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
8. 将自然数按照如图所示的规律排列,由图可知,第2行、第3列的数字是5,则第n行、第(n+1)列的数字是 (
A.$n^{2}+n$
B.$n^{2}+1$
C.$n^{2}+n-1$
D.$n^{2}+n+1$
C
)A.$n^{2}+n$
B.$n^{2}+1$
C.$n^{2}+n-1$
D.$n^{2}+n+1$
答案:
C
9. 观察图①月历中“阶梯框”中的数字规律,回答问题.
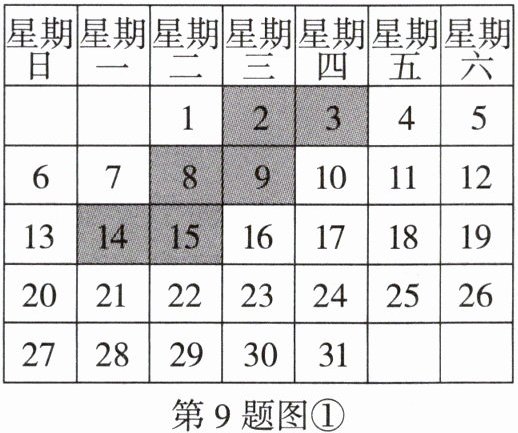
(1)像这样在任意一个月历中用“阶梯框”圈出六个数,如图②,请根据规律补全图②中的“阶梯框”的数字;
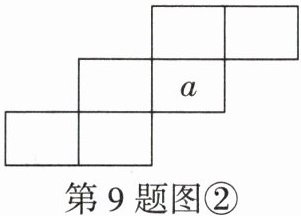
(2)①求图②“阶梯框”中6个数的和,并说明所求结果是3的倍数;
②请在图①中用虚线框框住(1)中a可能取的值.

(1)像这样在任意一个月历中用“阶梯框”圈出六个数,如图②,请根据规律补全图②中的“阶梯框”的数字;

(2)①求图②“阶梯框”中6个数的和,并说明所求结果是3的倍数;
②请在图①中用虚线框框住(1)中a可能取的值.
答案:
解:
(1)补全“阶梯框”如解图①;
(2)①6个数的和为$a - 7 + a - 6 + a - 1 + a + a + 5 + a + 6 = 6a - 3 = 3(2a - 1)$,所以这6个数的和是3的倍数;②如解图②,虚线框内为a可能取的值
解:
(1)补全“阶梯框”如解图①;

(2)①6个数的和为$a - 7 + a - 6 + a - 1 + a + a + 5 + a + 6 = 6a - 3 = 3(2a - 1)$,所以这6个数的和是3的倍数;②如解图②,虚线框内为a可能取的值

10. (教材数学活动改编)如果一个两位数的个位数是b,十位数是a,那么我们可以把这个两位数简记为$\overline {ab}$,即$\overline {ab}= 10a+b.$
【探究】设$\overline {abc}$是一个三位数,若$(a+b+c)$可以被3整除,则这个数可以被3整除.
解:$\overline {abc}= 100a+10b+c$
$=(
$=3(
显然
因为$(a+b+c)$可以被3整除,所以这个数可以被3整除.
(1)补全上面解题过程;
(2)设$\overline {abcd}$是一个四位数,若$a+b+c+d$可以被9整除,试说明这个四位数可以被9整除.
(3) 一个三位自然数$\overline {abc}$,若满足$a+c= b$,则称这个三位数为“位和数”,试说明:任意一个“位和数”都能被11整除.
【探究】设$\overline {abc}$是一个三位数,若$(a+b+c)$可以被3整除,则这个数可以被3整除.
解:$\overline {abc}= 100a+10b+c$
$=(
99a + 9b
)+ (a+b+c)$$=3(
33a + 3b
)+ (a+b+c).$显然
$3(33a + 3b)$
能被3整除,因为$(a+b+c)$可以被3整除,所以这个数可以被3整除.
(1)补全上面解题过程;
(2)设$\overline {abcd}$是一个四位数,若$a+b+c+d$可以被9整除,试说明这个四位数可以被9整除.
(3) 一个三位自然数$\overline {abc}$,若满足$a+c= b$,则称这个三位数为“位和数”,试说明:任意一个“位和数”都能被11整除.
(2)$\overline {abcd}=1000a + 100b + 10c + d=(999a + 99b + 9c)+(a + b + c + d)=9(111a + 11b + c)+(a + b + c + d)$,显然$9(111a + 11b + c)$能被9整除,因为$a + b + c + d$可以被9整除,所以这个四位数可以被9整除.
(3)因为$\overline {abc}$是“位和数”,所以$a + c = b$,因为$\overline {abc}=100a + 10b + c=99a + 10b + a + c=99a + 10b + b=99a + 11b=11(9a + b)$,显然$11(9a + b)$能被11整除,所以任意一个“位和数”都能被11整除.
(3)因为$\overline {abc}$是“位和数”,所以$a + c = b$,因为$\overline {abc}=100a + 10b + c=99a + 10b + a + c=99a + 10b + b=99a + 11b=11(9a + b)$,显然$11(9a + b)$能被11整除,所以任意一个“位和数”都能被11整除.
答案:
解:
(1)$99a + 9b;33a + 3b;3(33a + 3b)$;
(2)$\overline {abcd}=1000a + 100b + 10c + d=(999a + 99b + 9c)+(a + b + c + d)=9(111a + 11b + c)+(a + b + c + d)$,显然$9(111a + 11b + c)$能被9整除,因为$a + b + c + d$可以被9整除,所以这个四位数可以被9整除.
(3)因为$\overline {abc}$是“位和数”,所以$a + c = b$,因为$\overline {abc}=100a + 10b + c=99a + 10b + a + c=99a + 10b + b=99a + 11b=11(9a + b)$,显然$11(9a + b)$能被11整除,所以任意一个“位和数”都能被11整除.
(1)$99a + 9b;33a + 3b;3(33a + 3b)$;
(2)$\overline {abcd}=1000a + 100b + 10c + d=(999a + 99b + 9c)+(a + b + c + d)=9(111a + 11b + c)+(a + b + c + d)$,显然$9(111a + 11b + c)$能被9整除,因为$a + b + c + d$可以被9整除,所以这个四位数可以被9整除.
(3)因为$\overline {abc}$是“位和数”,所以$a + c = b$,因为$\overline {abc}=100a + 10b + c=99a + 10b + a + c=99a + 10b + b=99a + 11b=11(9a + b)$,显然$11(9a + b)$能被11整除,所以任意一个“位和数”都能被11整除.
查看更多完整答案,请扫码查看


