第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
24. 体育老师胸前总挂着一只停表,如图6所示.停表的短针是分针,转一圈的时间是15 min,则它的分度值是 (12)
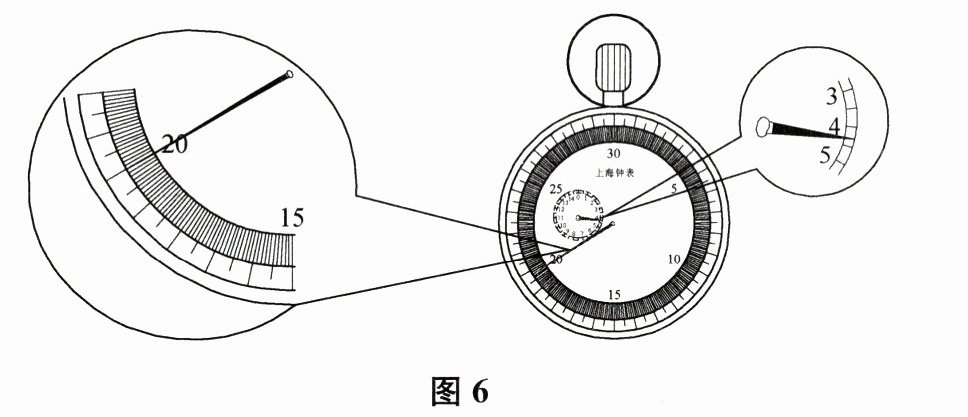
0.5
min.停表的长针是秒针,转一圈的时间是30 s,则它的分度值是 (13)0.1
s.根据图中分针和秒针的位置,应记录的时间为 (14)4min20s
.
答案:
解:
(12)0.5
(13)0.1
(14)4min20s
(12)0.5
(13)0.1
(14)4min20s
25. 如图7(a)所示,小明和小华两位同学想测量一卷筒纸的总长度,考虑到筒纸很长避免浪费,所以不可能将纸全部展开后再测量.两位同学经过讨论,提出了两种不同的测量方案.
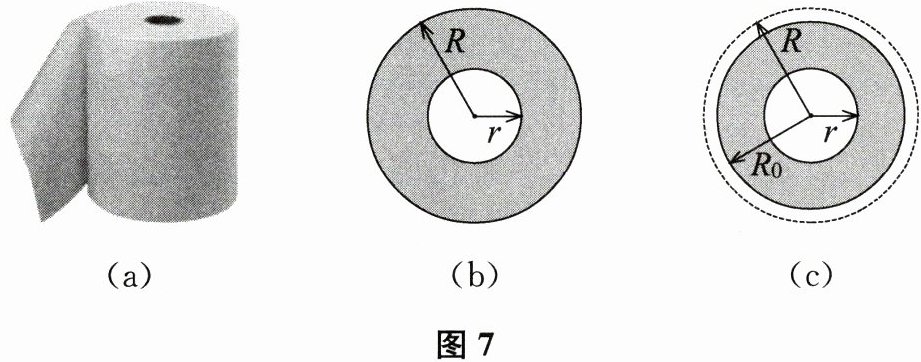
(1)小明的方案:首先从卷筒纸的标签上得知该型号卷筒纸纸张的厚度为d,然后测出卷筒纸的内半径为r,外半径为R,如图7(b)所示,则该卷筒纸的总长度为 (15) .
(2)小华的方案:首先测出卷筒纸的内半径为r,外半径为R,然后拉出适当长度的卷筒纸,测出它的长度为L₀,并再次测得此时卷筒纸的外半径减小到了R₀,如图7(c)所示,则该卷筒纸的总长度为 (16) .

(1)小明的方案:首先从卷筒纸的标签上得知该型号卷筒纸纸张的厚度为d,然后测出卷筒纸的内半径为r,外半径为R,如图7(b)所示,则该卷筒纸的总长度为 (15) .
(2)小华的方案:首先测出卷筒纸的内半径为r,外半径为R,然后拉出适当长度的卷筒纸,测出它的长度为L₀,并再次测得此时卷筒纸的外半径减小到了R₀,如图7(c)所示,则该卷筒纸的总长度为 (16) .
答案:
【解析】:
(1)小明的方案:不可能把纸全部拉直进行测量,但可以测出整卷纸的内外半径,从而根据圆的面积公式计算出纸的总体积,再除以纸的厚度,就可以得到纸的总长度。设该卷筒纸的总长度为$L$,由于纸的厚度为$d$,纸的宽度(即卷筒纸的高度)设为$h$(此处在计算中不需要具体数值,因为会约去),则根据体积公式,整卷纸的体积可以表示为$V = L × d × h$(这里$h$在后续计算中会被约去,因为内外圆的面积差中已经隐含了高度$h$)。另一方面,整卷纸的体积也可以看作是大圆面积减去小圆面积后乘以高度$h$,即$V = \pi(R^{2} - r^{2})h$。将两个体积表达式相等,得到$L × d × h = \pi(R^{2} - r^{2})h$,由于$h$在等式两边都存在且不为零,可以约去,得到$L = \frac{\pi(R^{2} - r^{2})}{d}$。
(2)小华的方案:首先测出整卷纸的内外半径,然后拉出一段纸,测出其长度和此时卷筒纸的外半径。设该卷筒纸的总长度为$L$,未拉出时卷筒纸的体积为$\pi(R^{2} - r^{2})h$(同样,$h$在后续计算中会被约去)。拉出一段纸后,剩余卷筒纸的体积为$\pi(R_{0}^{2} - r^{2})h$。因此,拉出的那部分纸的体积就是两者之差,即$\pi(R^{2} - R_{0}^{2})h$。由于拉出的纸的长度为$L_{0}$,厚度为$d$,所以其体积也可以表示为$L_{0} × d × h$。将两个体积表达式相等,得到$L_{0} × d × h = \pi(R^{2} - R_{0}^{2})h$,同样地,$h$在等式两边都存在且不为零,可以约去,得到$L = \frac{\pi(R^{2} - r^{2})d}{R^{2} - R_{0}^{2}} × L_{0} = \frac{\pi(R^{2} - r^{2})}{R^{2} - R_{0}^{2}}L_{0}$(这里的$L$表示总长度,是通过比例关系得出的,即总长度与拉出的长度之比等于总体积与拉出的体积之比)。
【答案】:
(1)$\frac{\pi(R^{2} - r^{2})}{d}$;
(2)$\frac{\pi(R^{2} - r^{2})}{R^{2} - R_{0}^{2}}L_{0}$。
(1)小明的方案:不可能把纸全部拉直进行测量,但可以测出整卷纸的内外半径,从而根据圆的面积公式计算出纸的总体积,再除以纸的厚度,就可以得到纸的总长度。设该卷筒纸的总长度为$L$,由于纸的厚度为$d$,纸的宽度(即卷筒纸的高度)设为$h$(此处在计算中不需要具体数值,因为会约去),则根据体积公式,整卷纸的体积可以表示为$V = L × d × h$(这里$h$在后续计算中会被约去,因为内外圆的面积差中已经隐含了高度$h$)。另一方面,整卷纸的体积也可以看作是大圆面积减去小圆面积后乘以高度$h$,即$V = \pi(R^{2} - r^{2})h$。将两个体积表达式相等,得到$L × d × h = \pi(R^{2} - r^{2})h$,由于$h$在等式两边都存在且不为零,可以约去,得到$L = \frac{\pi(R^{2} - r^{2})}{d}$。
(2)小华的方案:首先测出整卷纸的内外半径,然后拉出一段纸,测出其长度和此时卷筒纸的外半径。设该卷筒纸的总长度为$L$,未拉出时卷筒纸的体积为$\pi(R^{2} - r^{2})h$(同样,$h$在后续计算中会被约去)。拉出一段纸后,剩余卷筒纸的体积为$\pi(R_{0}^{2} - r^{2})h$。因此,拉出的那部分纸的体积就是两者之差,即$\pi(R^{2} - R_{0}^{2})h$。由于拉出的纸的长度为$L_{0}$,厚度为$d$,所以其体积也可以表示为$L_{0} × d × h$。将两个体积表达式相等,得到$L_{0} × d × h = \pi(R^{2} - R_{0}^{2})h$,同样地,$h$在等式两边都存在且不为零,可以约去,得到$L = \frac{\pi(R^{2} - r^{2})d}{R^{2} - R_{0}^{2}} × L_{0} = \frac{\pi(R^{2} - r^{2})}{R^{2} - R_{0}^{2}}L_{0}$(这里的$L$表示总长度,是通过比例关系得出的,即总长度与拉出的长度之比等于总体积与拉出的体积之比)。
【答案】:
(1)$\frac{\pi(R^{2} - r^{2})}{d}$;
(2)$\frac{\pi(R^{2} - r^{2})}{R^{2} - R_{0}^{2}}L_{0}$。
26. 某小组同学在探究摆球摆动的周期(摆球来回摆动一次的时间)与哪些因素有关,他们用两个质量不同的小球制作了不同摆线长度的摆进行实验,如图8所示.表一记录了他们实验时的部分数据.
表一
|实验序号|摆球质量m/g|摆线长度l/m|摆动的最大距离s/m|摆动10次的时间t/s|
|1|20|0.8|0.10|18|
|2|20|1.0|0.14|20|
|3|20|1.2|0.10|22|
|4|30|1.0|0.14|20|
|5|30|1.0|0.10|20|
(1)序号1中摆的摆动周期是 (17) s.序号 (18) 中摆的摆动周期相同.
(2)分析比较序号2和4中的数据可发现:摆动周期与 (19) 无关.分析比较序号4和5中的数据可发现:摆动周期与 (20) 无关.
(3)分析序号1与3中的数据可知: (21) .
(4)为了验证(3)的结论是否具有普遍性,请在表二再设计一次拟进行的实验,使之能与序号1与3的数据进行对照.
表二
|实验序号|摆球质量m/g|摆线长度l/m|摆动的最大距离s/m|摆动10次的时间t/s|
|6| (22) | (23) | (24) | \ |
表一
|实验序号|摆球质量m/g|摆线长度l/m|摆动的最大距离s/m|摆动10次的时间t/s|
|1|20|0.8|0.10|18|
|2|20|1.0|0.14|20|
|3|20|1.2|0.10|22|
|4|30|1.0|0.14|20|
|5|30|1.0|0.10|20|
(1)序号1中摆的摆动周期是 (17) s.序号 (18) 中摆的摆动周期相同.
(2)分析比较序号2和4中的数据可发现:摆动周期与 (19) 无关.分析比较序号4和5中的数据可发现:摆动周期与 (20) 无关.
(3)分析序号1与3中的数据可知: (21) .
(4)为了验证(3)的结论是否具有普遍性,请在表二再设计一次拟进行的实验,使之能与序号1与3的数据进行对照.
表二
|实验序号|摆球质量m/g|摆线长度l/m|摆动的最大距离s/m|摆动10次的时间t/s|
|6| (22) | (23) | (24) | \ |
答案:
【解析】:
本题主要考查了控制变量法的应用及实验数据的分析。
(1)需要计算摆的摆动周期,这涉及到简单的除法运算。
(2)通过对比不同实验序号的数据,来探究摆动周期与摆球质量、摆线长度以及摆动的最大距离之间的关系,这需要理解和应用控制变量的方法。
(3)通过实验数据来总结物理规律,即摆动周期与摆线长度的关系。
(4)根据实验目的和已做的实验数据,来设计新的实验以验证规律的普遍性,这需要实验设计和逻辑推理能力。
【答案】:
(1)摆动周期是摆球来回摆动一次的时间,所以序号1中摆的摆动周期$T = \frac{t}{n} = \frac{18}{10} = 1.8s$($t$为摆动$10$次的时间,$n$为摆动次数)。
对比各次实验可知,序号$2$、$4$与$5$中,摆动$10$次的时间均为$20s$,即摆动周期相同。
所以答案为$1.8$ ;$2$、$4$与$5$。
(2)分析比较序号$2$和$4$中的数据,摆球质量不同,但摆动周期相同,说明摆动周期与摆球质量无关。
分析比较序号$4$和$5$中的数据,摆动的最大距离不同,但摆动周期相同,说明摆动周期与摆动的最大距离无关。
所以答案为摆球质量;摆动的最大距离。
(3)分析序号$1$与$3$中的数据,摆球质量相同,摆动的最大距离也相同,而摆线长度不同,且摆线长度越长,摆动周期越大。
所以答案为在摆球质量和摆动的最大距离相同的情况下,摆线长度越长,摆动周期越大。
(4)为了验证
(3)的结论是否具有普遍性,需要控制摆球质量和摆动的最大距离相同,只改变摆线长度进行实验。
所以答案可以为$20$;$1.4$;$0.10$。(答案不唯一,只要摆球质量和摆动的最大距离与序号$1$或$3$相同,摆线长度不同即可)
本题主要考查了控制变量法的应用及实验数据的分析。
(1)需要计算摆的摆动周期,这涉及到简单的除法运算。
(2)通过对比不同实验序号的数据,来探究摆动周期与摆球质量、摆线长度以及摆动的最大距离之间的关系,这需要理解和应用控制变量的方法。
(3)通过实验数据来总结物理规律,即摆动周期与摆线长度的关系。
(4)根据实验目的和已做的实验数据,来设计新的实验以验证规律的普遍性,这需要实验设计和逻辑推理能力。
【答案】:
(1)摆动周期是摆球来回摆动一次的时间,所以序号1中摆的摆动周期$T = \frac{t}{n} = \frac{18}{10} = 1.8s$($t$为摆动$10$次的时间,$n$为摆动次数)。
对比各次实验可知,序号$2$、$4$与$5$中,摆动$10$次的时间均为$20s$,即摆动周期相同。
所以答案为$1.8$ ;$2$、$4$与$5$。
(2)分析比较序号$2$和$4$中的数据,摆球质量不同,但摆动周期相同,说明摆动周期与摆球质量无关。
分析比较序号$4$和$5$中的数据,摆动的最大距离不同,但摆动周期相同,说明摆动周期与摆动的最大距离无关。
所以答案为摆球质量;摆动的最大距离。
(3)分析序号$1$与$3$中的数据,摆球质量相同,摆动的最大距离也相同,而摆线长度不同,且摆线长度越长,摆动周期越大。
所以答案为在摆球质量和摆动的最大距离相同的情况下,摆线长度越长,摆动周期越大。
(4)为了验证
(3)的结论是否具有普遍性,需要控制摆球质量和摆动的最大距离相同,只改变摆线长度进行实验。
所以答案可以为$20$;$1.4$;$0.10$。(答案不唯一,只要摆球质量和摆动的最大距离与序号$1$或$3$相同,摆线长度不同即可)
查看更多完整答案,请扫码查看


