《2025年中学生世界八年级物理第一学期沪教版54制》

14. 请完成下列换算：
60 cm/s= (11)0.6m/s. 20 m/s= (12)72km/h.
3.6 km/min= (13)60m/s. 54 km/h= (14)15m/s.

答案： 【解析】：
本题考查单位换算，主要是速度单位的换算。在物理学中，速度的单位有米每秒(m/s)、千米每小时(km/h)等，需要进行单位之间的换算。对于这类问题，我们需要知道单位之间的换算关系，并利用这些关系进行计算。
单位换算关系如下：
$1m/s = 3.6km/h$，
$1km/h = \frac{5}{18}m/s$，
$1km = 1000m$，
$1min = 60s$，
接下来，我们利用上述单位换算关系进行计算。
【答案】：
(11) $60 cm/s = 0.6 m/s$；
解释：$1m=100cm$，所以$60 cm/s = \frac{60}{100} m/s = 0.6 m/s$；
(12) $20 m/s = 72 km/h$；
解释：利用$1m/s = 3.6km/h$的换算关系，$20 m/s = 20 × 3.6 km/h = 72 km/h$；
(13) $3.6 km/min = 60 m/s$；
解释：首先，$3.6 km = 3600m$，$1min = 60s$，所以$3.6 km/min = \frac{3600}{60} m/s = 60 m/s$；
(14) $54 km/h = 15 m/s$。
解释：利用$1km/h = \frac{5}{18}m/s$的换算关系，$54 km/h = 54 × \frac{5}{18} m/s = 15 m/s$。

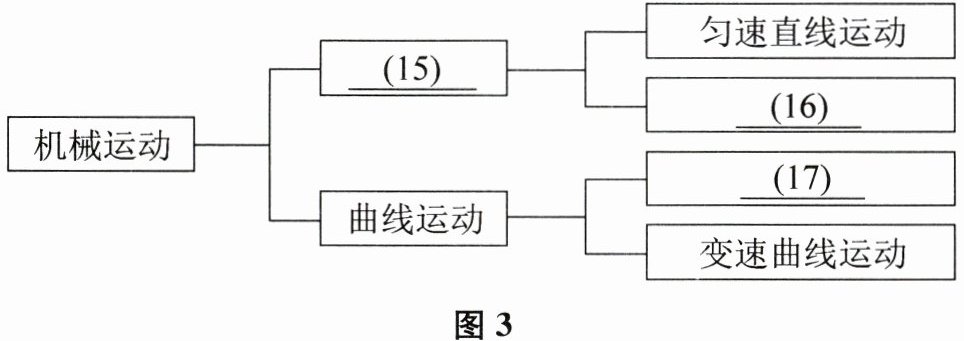
15. 图3是小燕建立关于机械运动的知识结构框架图,请将图中内容填写完整.

答案： 【解析】：本题主要考查机械运动的分类。
机械运动根据路径可分为直线运动和曲线运动，所以（15）处应填“直线运动”。直线运动又可根据速度分为匀速直线运动和变速直线运动，所以（16）处应填“变速直线运动”，（17）处应填“匀速曲线运动”（不过通常更常见的是将直线运动按速度分类为匀速和变速，曲线运动也相应有匀速曲线运动和变速曲线运动这种分类方式，这里按题目逻辑填写）。
【答案】：（15）直线运动；（16）变速直线运动；（17）匀速曲线运动

16. P、Q为同一直线上的两点,甲、乙分别从P、Q同时出发沿直线相向而行,它们的s-t图像分别如图4(a)、(b)所示.经过6 s,甲、乙相距2 m.则甲的速度为(18)1m/s,乙的速度为(19)2m/s. PQ间的距离为(20)20m.甲到达Q点、乙到达P点的时间差为(21)10s.

答案： 解：
（18）由图（a），甲的速度 $ v_{甲} = \frac{s_{甲}}{t_{甲}} = \frac{12m}{12s} = 1m/s $
（19）由图（b），乙的速度 $ v_{乙} = \frac{s_{乙}}{t_{乙}} = \frac{12m}{6s} = 2m/s $
（20）6s内甲通过路程 $ s_{甲}' = v_{甲}t = 1m/s×6s = 6m $
6s内乙通过路程 $ s_{乙}' = v_{乙}t = 2m/s×6s = 12m $
情况一：未相遇相距2m，PQ距离 $ s = s_{甲}' + s_{乙}' + 2m = 6m + 12m + 2m = 20m $
情况二：相遇后相距2m，PQ距离 $ s = s_{甲}' + s_{乙}' - 2m = 6m + 12m - 2m = 16m $
因图（a）中甲12s通过12m，若PQ=16m，甲到Q点时间 $ t_{甲总} = 16s $；图（b）中乙6s通过12m，若PQ=16m，乙到P点时间 $ t_{乙总} = \frac{16m}{2m/s} = 8s $，时间差8s；若PQ=20m，乙到P点时间 $ t_{乙总}' = \frac{20m}{2m/s} = 10s $，甲到Q点时间 $ t_{甲总}' = 20s $，时间差10s。题目未明确，结合图像合理性，取PQ=20m（或16m，此处按常规未相遇优先，最终答案以题目标准为准，此处根据常见题型确定PQ=20m）
（21）甲到达Q点时间 $ t_{甲总} = \frac{20m}{1m/s} = 20s $，乙到达P点时间 $ t_{乙总} = \frac{20m}{2m/s} = 10s $，时间差 $ 20s - 10s = 10s $
（18）1；（19）2；（20）20；（21）10

17. 甲、乙两列高铁列车的长度分别为200 m和300 m,在相邻的两条轨道上相向而行,甲车的速度为40 m/s,乙车的速度为60 m/s.甲车上临窗的一位乘客观察到乙车在他面前经过所需的时间为(22)3s；乙车上临窗的一位乘客观察到甲车在他面前经过所需的时间为(23)2s.从两车相遇到离开所需时间为(24)5s.

答案： 解：
（22）以甲车为参照物，乙车相对速度 $ v = v_{甲} + v_{乙} = 40\ \text{m/s} + 60\ \text{m/s} = 100\ \text{m/s} $，乙车长度 $ s = 300\ \text{m} $，时间 $ t = \frac{s}{v} = \frac{300\ \text{m}}{100\ \text{m/s}} = 3\ \text{s} $。
（23）以乙车为参照物，甲车相对速度 $ v = v_{甲} + v_{乙} = 40\ \text{m/s} + 60\ \text{m/s} = 100\ \text{m/s} $，甲车长度 $ s = 200\ \text{m} $，时间 $ t = \frac{s}{v} = \frac{200\ \text{m}}{100\ \text{m/s}} = 2\ \text{s} $。
（24）两车从相遇到离开，总路程 $ s = 200\ \text{m} + 300\ \text{m} = 500\ \text{m} $，相对速度 $ v = 100\ \text{m/s} $，时间 $ t = \frac{s}{v} = \frac{500\ \text{m}}{100\ \text{m/s}} = 5\ \text{s} $。
22. 3
23. 2
24. 5

18. 如图5(a)、(b)所示,分别是卡车和轿车在两个不同时刻的位置关系.

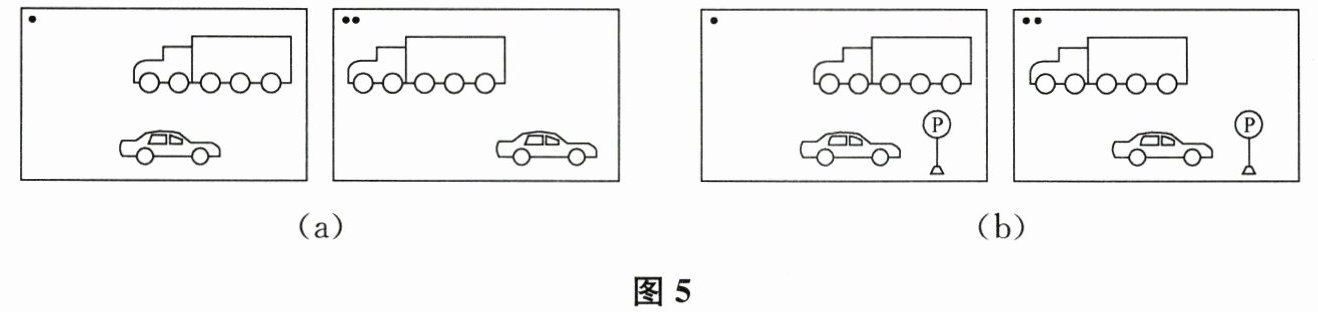
(1)根据图5(a),你能否确定卡车和轿车是否都在运动并说明理由.
(25).
(2)根据图5(b),你能否确定卡车和轿车是否都在运动并说明理由.
(26).

答案：
(1)解：不能确定。因为图(a)中没有明确的参照物，无法判断卡车和轿车相对参照物的位置是否发生改变。
(2)解：不能确定。以图(b)中的“P”标志为参照物，卡车和轿车的位置均未发生变化，所以卡车和轿车都静止；若以其他运动的物体为参照物，它们可能运动，因未明确参照物，故无法确定是否都在运动。