《2025年中学生世界八年级物理第一学期沪教版54制》

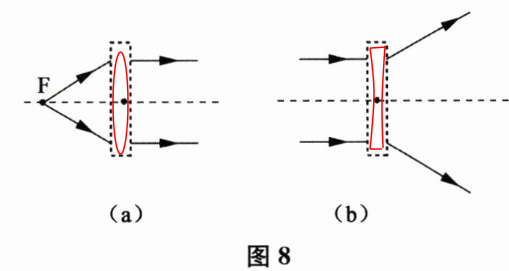
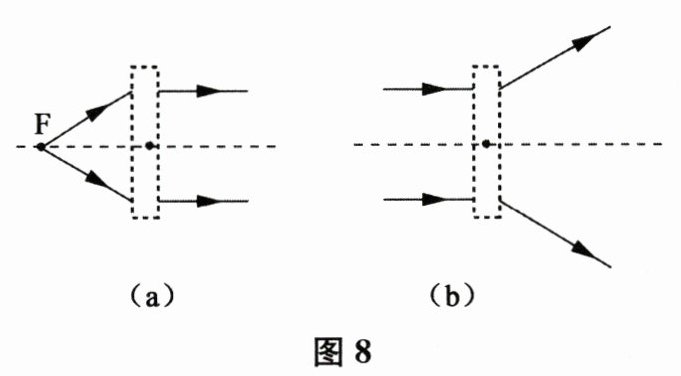
20. 在图 8(a)、(b)中,画出了光通过透镜前后的方向,请在虚线框中填上适当的透镜。

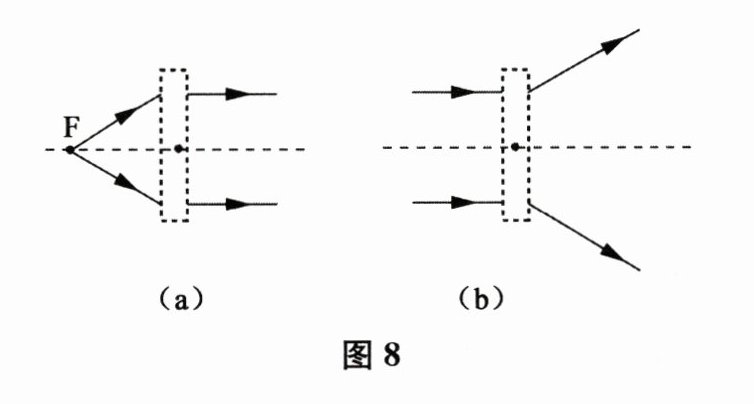
答案：

21. 请根据平面镜成像特点在图 9 中画出物体 AB 在平面镜中的像 A'B'。

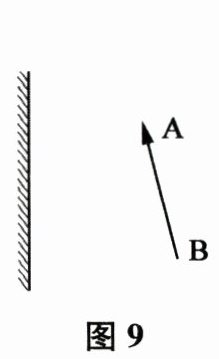
答案： 【解析】：
本题考查平面镜成像特点以及根据此特点来画出物体在平面镜中的像。平面镜成像特点为：像与物大小相等、像与物到平面镜的距离相等、像与物的连线与镜面垂直，即像与物关于平面镜对称。我们可以利用对称的性质，通过作出物体端点$A$、$B$关于平面镜的对称点$A'$、$B'$，然后连接$A'$、$B'$来得到物体$AB$在平面镜中的像$A'B'$。
具体步骤如下：
1. 过$A$点作平面镜的垂线，垂足为$O_1$，延长$AO_1$至$A'$，使$A'O_1 = AO_1$，则$A'$就是$A$在平面镜中的像。
2. 过$B$点作平面镜的垂线，垂足为$O_2$，延长$BO_2$至$B'$，使$B'O_2 = BO_2$，则$B'$就是$B$在平面镜中的像。
3. 连接$A'$、$B'$，得到物体$AB$在平面镜中的像$A'B'$。
【答案】：
图略（按照上述步骤作出$A$、$B$关于平面镜的对称点$A'$、$B'$，连接$A'$、$B'$即可得到物体$AB$在平面镜中的像$A'B'$）。

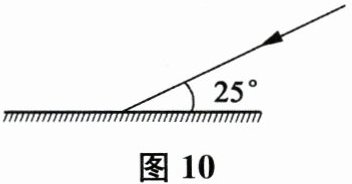
22. 在图 10 中,根据给出的入射光线画出反射光线,并标出反射角的大小。

答案： 【解析】：
本题主要考查光的反射定律的应用，特别是反射光线和反射角的确定。根据光的反射定律，反射光线、入射光线和法线都在同一平面内，反射光线和入射光线分居法线两侧，反射角等于入射角。题目中给出了入射光线和入射角的大小，我们需要根据这些信息来画出反射光线，并标出反射角的大小。
首先，确定法线的位置，法线是入射点和镜面垂直的线。然后，根据入射角的大小，在法线的另一侧画出反射光线，使得反射角等于入射角。最后，在图上标出反射角的大小。
【答案】：
图略（由于无法直接画图，这里用文字描述）。
1. 首先，在入射点处画出与镜面垂直的法线。
2. 然后，在法线的另一侧，根据入射角（假设为$40^\circ$，具体角度根据题目给出的入射光线确定）画出反射光线，使得反射角等于入射角，即$40^\circ$。
3. 在反射光线与法线的夹角处标出反射角的大小，即$40^\circ$。

23. 如图 11 所示,S'是发光点 S 在平面镜中所成的像,请作出平面镜 MN。

答案： 【解析】：
本题考查平面镜成像的特点，即像与物关于平面镜对称。通过连接发光点$S$和其像点$S'$，作这条连线的垂直平分线，即为平面镜的位置。
具体步骤如下：
1. 连接发光点$S$和像点$S'$，得到线段$SS'$。
2. 作线段$SS'$的垂直平分线，这条垂直平分线就是平面镜$MN$的位置。
【答案】：
1. 连接$S$和$S'$，得到线段$SS'$。
2. 作线段$SS'$的垂直平分线，标记为$MN$。
图略。

24. 从地球向月球发出一束激光,经 2.56 s 收到从月球表面反射回来的激光,求地球和月球之间的距离。

答案： 【解析】：本题主要考查速度公式在光传播问题中的应用。
首先，需要知道光在真空中的传播速度，这是解题的基础。
其次，根据题目给出的激光往返时间，可以计算出激光从地球到月球的单程时间。
最后，利用速度公式$s = vt$（路程等于速度乘以时间）计算出地球和月球之间的距离。
【答案】：
光在真空中的传播速度$v = 3 × 10^{8} m/s$。
激光往返地球和月球的总时间$t_{总} = 2.56s$，
所以激光从地球到月球的单程时间$t = \frac{1}{2}t_{总} = \frac{1}{2} × 2.56 = 1.28s$。
根据速度公式，地球和月球之间的距离$s = vt = 3 × 10^{8} × 1.28 = 3.84 × 10^{8} m = 3.84 × 10^{5} km$。
所以，地球和月球之间的距离是$3.84 × 10^{5} km$。