1. 有下列函数:①$y = 5x$;②$y = 2x - 1$;③$y = \frac{3}{x}$;④$y = \frac{1}{3}x + 3$;⑤$y = x^{2} - 2x + 1$,其中是一次函数的有 [教材 P37 练习 T1 变式](
A.1 个
B.2 个
C.3 个
D.4 个
C
)A.1 个
B.2 个
C.3 个
D.4 个
答案:
C
2. 若正比例函数$y = (m - 1)x$的图象从左到右逐渐上升,则$m$的取值范围是
m>1
.[教材 P37 练习 T2 变式 1]
答案:
m>1
3. 已知点$A(x_{1},x_{2})$,$B(x_{2},y_{2})是函数y = - 5x$图象上的两个点,若$x_{1} - x_{2} < 0$,则$y_{1}$
>
$y_{2}$.(填“$>$”“$<$”或“$=$”)[教材 P37 练习 T2 变式 2]
答案:
>
4. 如图,正比例函数$y = kx$,$y = mx$,$y = nx$在同一平面直角坐标系中的图象如图所示,则比例系数$k$,$m$,$n$的大小关系是
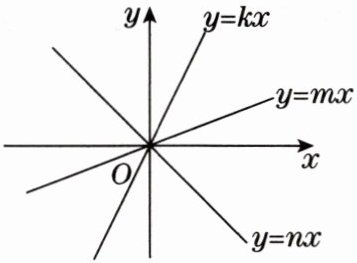
k>m>n
.[教材 P37 练习 T3 变式]
答案:
k>m>n
5. 已知函数$y = (n + 1)x + |n| - 1$.[教材 P35 定义变式]
(1) 若该函数为一次函数,则$n$的取值范围为
(2) 若该函数为正比例函数,则$n$的值为
(1) 若该函数为一次函数,则$n$的取值范围为
n≠-1
;(2) 若该函数为正比例函数,则$n$的值为
1
.
答案:
(1)n≠-1
(2)1
(1)n≠-1
(2)1
6. 画出正比例函数$y = -\frac{1}{3}x$,$y = 3x$的图象,并分别指出其经过哪些象限.[教材 P35 例 1 变式]
答案:
解:画图略.正比例函数$y=-\dfrac{1}{3}x$的图象经过第二、四象限,正比例函数y=3x的图象经过第一、三象限.
查看更多完整答案,请扫码查看


