1. 在直角三角形中,若一个锐角是$35^{\circ}$,则该直角三角形的另一个锐角是 [教材P79推论1变式1](
A.$35^{\circ}$
B.$45^{\circ}$
C.$55^{\circ}$
D.$65^{\circ}$
C
)A.$35^{\circ}$
B.$45^{\circ}$
C.$55^{\circ}$
D.$65^{\circ}$
答案:
C
2. 在$\triangle ABC$中,$\angle A= \angle B+\angle C$,则该三角形是 [教材P79推论2变式1](
A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法确定
B
)A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法确定
答案:
B
3. 如图,$\triangle ABC$被撕去了一角,测量得$\angle A= 58^{\circ}$,$\angle B= 32^{\circ}$,则$\triangle ABC$是

直角
三角形.(填“锐角”“直角”或“钝角”)[教材P79推论2变式2]
答案:
直角
4. 如图,已知$\angle A= 32^{\circ}$,$\angle ADC= 110^{\circ}$,$BE\perp AC于点E$,则$\angle B$的度数为

52°
. [教材P79推论1变式2]
答案:
52°
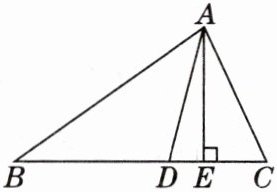
5. 如图,在$\triangle ABC$中,$AE是\triangle ABC$的高,$AD平分\angle BAC$,$\angle B= 35^{\circ}$,$\angle C= 65^{\circ}$,求$\angle DAE$的度数. [教材P87复习题A组T9变式]

答案:
解:在$\triangle ABC$中,$\angle BAC=180^{\circ}-\angle B-\angle C=180^{\circ}-35^{\circ}-65^{\circ}=80^{\circ}$.
∵AD平分$\angle BAC$,
∴$\angle BAD=\frac{1}{2}\angle BAC=\frac{1}{2}×80^{\circ}=40^{\circ}$.
∵AE是$\triangle ABC$的高,
∴$\angle AEB=90^{\circ}$,
在$\triangle ABE$中,$\angle BAE=90^{\circ}-\angle B=90^{\circ}-35^{\circ}=55^{\circ}$.
∴$\angle DAE=\angle BAE-\angle BAD=55^{\circ}-40^{\circ}=15^{\circ}$.
答:$\angle DAE$的度数为$15^{\circ}$.
∵AD平分$\angle BAC$,
∴$\angle BAD=\frac{1}{2}\angle BAC=\frac{1}{2}×80^{\circ}=40^{\circ}$.
∵AE是$\triangle ABC$的高,
∴$\angle AEB=90^{\circ}$,
在$\triangle ABE$中,$\angle BAE=90^{\circ}-\angle B=90^{\circ}-35^{\circ}=55^{\circ}$.
∴$\angle DAE=\angle BAE-\angle BAD=55^{\circ}-40^{\circ}=15^{\circ}$.
答:$\angle DAE$的度数为$15^{\circ}$.
查看更多完整答案,请扫码查看


