《2025年点拨训练八年级数学上册沪科版安徽专版》

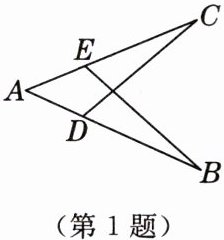
1. 如图,$\angle B= \angle C$,利用“AAS”,证$\triangle ABE\cong\triangle ACD$,则可添加的一个条件是AE=AD(答案不唯一).[教材P105练习T2变式]

答案： AE=AD(答案不唯一)

2. 下列有关三角形全等的判定,正确的是[教材P103探究变式](B)
A.三角分别相等的两个三角形全等
B.两角和其中一角的对边分别相等的两个三角形全等
C.一边和一角分别相等的两个三角形全等
D.两边及其中一边的对角对应相等的两个三角形全等

答案： B

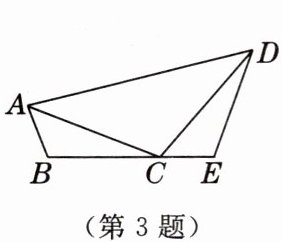
3. 如图,在$\triangle ABC和\triangle CDE$中,点$B$,$C$,$E$在同一条直线上,$\angle B= \angle E= \angle ACD$,$AC= CD$.若$AB= 2$,$BE= 6$,则$DE$的长为(C)

A.8
B.6
C.4
D.2

答案： C

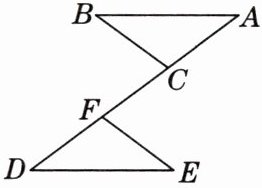
4. 如图,$AB// DE$,点$C$,$F在线段AD$上,且$AC= DF$,$\angle B= \angle E$.求证：$\triangle ABC\cong\triangle DEF$.[教材P104例6变式]

答案： 证明：
∵AB//DE，
∴∠A=∠D.在△ABC和△DEF中，
∵∠A=∠D，∠B=∠E，AC=DF，
∴△ABC≌△DEF(AAS).