1.一个三角形三个内角的度数之比为$1:2:5$,则这个三角形一定是 [教材P68练习T1(1)变式]
(
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不确定
(
C
)A.锐角三角形
B.直角三角形
C.钝角三角形
D.不确定
答案:
C
2.在$\triangle ABC$中,$\angle A= 40^{\circ}$,$3\angle B= \angle C$,则$\angle C= $
105
$^{\circ}$. [教材P68练习T1(2)变式]
答案:
105
3.如图,点E,D分别在$AB$,$AC$上,$\angle B= 28^{\circ}$,$\angle C= 61^{\circ}$,则$\angle1+\angle2$的度数为
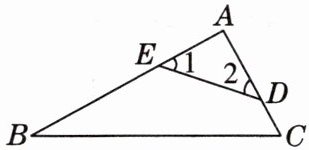
89°
. [教材P68练习T3变式]
答案:
89°
4.满足条件$\angle A= 2\angle B= 2\angle C的\triangle ABC$,它最大的角的度数是
90°
,因此这是一个直角
三角形(填“锐角”“直角”或“钝角”). [教材P71习题T2变式]
答案:
90°;直角
5.如图,在$\triangle ABC$中,$\angle B= 2\angle A$,$\angle C= \angle B+40^{\circ}$.求$\triangle ABC$的各内角度数. [教材P72习题T5变式]

答案:
解:因为∠B=2∠A,∠C=∠B+40°,∠A+∠B+∠C=180°,所以∠A+2∠A+2∠A+40°=180°,解得∠A=28°,所以∠B=2∠A=56°,∠C=∠B+40°=96°.
查看更多完整答案,请扫码查看


