《2025年点拨训练八年级数学上册沪科版安徽专版》

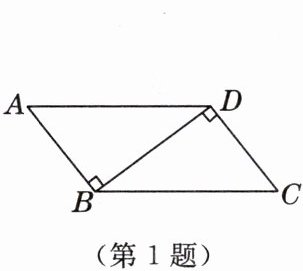
1. 如图,在四边形 $ABCD$ 中,连接 $BD$,且 $AB\perp BD$,$CD\perp BD$,若用“$HL$”判定 $Rt\triangle ABD$ 和 $Rt\triangle CDB$ 全等,则需要添加的条件是 [教材P107练习T3变式](D)

A.$\angle A= \angle C$
B.$\angle ADB= \angle CBD$
C.$AB = CD$
D.$AD = CB$

答案： D

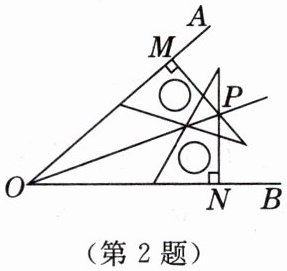
2. 如图,在$\angle AOB$的两边 $OA$,$OB$ 上分别取 $OM = ON$,再分别过点 $M$,$N$ 作 $OA$,$OB$ 的垂线,两垂线交点为 $P$,画射线 $OP$,则根据HL判定Rt△OMP≌Rt△ONP,进而得到 $OP$ 平分 $\angle AOB$。[教材P107练习T2变式]

答案： HL;Rt△OMP≌Rt△ONP

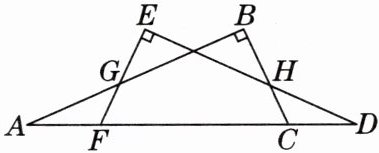
3. 如图,$Rt\triangle ABC$ 与 $Rt\triangle DEF$ 的顶点 $A$,$F$,$C$,$D$ 在同一条直线上,$AB$ 与 $EF$ 交于点 $G$,$BC$ 与 $DE$ 交于点 $H$,$\angle B= \angle E = 90^{\circ}$,$AF = CD$,$AB = DE$。求证：$Rt\triangle ABC\cong Rt\triangle DEF$。[教材P106例7变式]

答案： 证明：
∵AF=CD,
∴AF+FC=CD+CF，即AC=DF.在Rt△ABC和Rt△DEF中，
∵{AC=DF,AB=DE,
∴Rt△ABC≌Rt△DEF(HL).