1. 下列说法中,正确的是 [教材P71练习T2变式](
A.三角形的中线就是过顶点平分对边的直线
B.三角形的高就是顶点到对边的垂线
C.三角形的角平分线就是三角形的内角平分线
D.三角形的三条中线交于一点
D
)A.三角形的中线就是过顶点平分对边的直线
B.三角形的高就是顶点到对边的垂线
C.三角形的角平分线就是三角形的内角平分线
D.三角形的三条中线交于一点
答案:
D
2. 如图,在$\triangle ABC$中,$CD平分\angle ACB交AB于点D$,过点$D作DE// BC交AC于点E$. 若$\angle A= 50^{\circ}$,$\angle B= 60^{\circ}$,则$\angle CDE$的度数为 [教材P72习题T6变式](
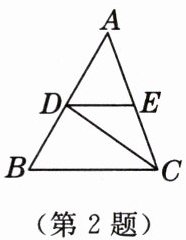
A.$45^{\circ}$
B.$40^{\circ}$
C.$30^{\circ}$
D.$35^{\circ}$
D
)
A.$45^{\circ}$
B.$40^{\circ}$
C.$30^{\circ}$
D.$35^{\circ}$
答案:
D
3. 如图,在$\triangle ABC$中,$AB= 10$,$AC= 8$,$D是BC$边的中点,连接$AD$. 若$\triangle ACD的周长为20$,则$\triangle ABD$的周长是
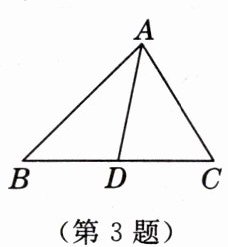
22
. [教材P72习题T4变式]
答案:
22
4. 如图,在$\triangle ABC$中,$\angle A= 60^{\circ}$,$BO$,$CO分别是\angle ABC和\angle ACB$的平分线,则$\angle BOC$的度数为
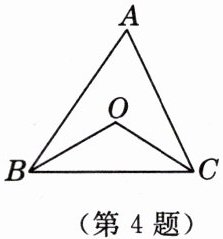
120°
. [教材P87复习题A组T5变式]
答案:
120°
5. 如图,在$\triangle ABC$中,$AE$,$CD是\triangle ABC$的两条高,$AB= 6$,$CD= 3$. [教材P71练习T3变式]
(1) 请画出$AE$,$CD$;
(2) 若$AE= 4$,求$BC$的长.
(1) 请画出$AE$,$CD$;
(2) 若$AE= 4$,求$BC$的长.

答案:
1. (1)
画法:过点$A$作$BC$的垂线,垂足为$E$,则$AE$为$\triangle ABC$的高;过点$C$作$AB$的垂线,垂足为$D$,则$CD$为$\triangle ABC$的高。
2. (2)
解:
根据三角形面积公式$S = \frac{1}{2}ah$($a$为底,$h$为这条底对应的高)。
因为$S_{\triangle ABC}=\frac{1}{2}AB\cdot CD$,且$S_{\triangle ABC}=\frac{1}{2}BC\cdot AE$。
已知$AB = 6$,$CD = 3$,$AE = 4$。
由$\frac{1}{2}AB\cdot CD=\frac{1}{2}BC\cdot AE$可得:
$AB\cdot CD=BC\cdot AE$。
把$AB = 6$,$CD = 3$,$AE = 4$代入$AB\cdot CD=BC\cdot AE$中,得到$6×3 = 4× BC$。
则$BC=\frac{6×3}{4}=\frac{18}{4}=\frac{9}{2}$。
所以$BC$的长为$\frac{9}{2}$。
画法:过点$A$作$BC$的垂线,垂足为$E$,则$AE$为$\triangle ABC$的高;过点$C$作$AB$的垂线,垂足为$D$,则$CD$为$\triangle ABC$的高。
2. (2)
解:
根据三角形面积公式$S = \frac{1}{2}ah$($a$为底,$h$为这条底对应的高)。
因为$S_{\triangle ABC}=\frac{1}{2}AB\cdot CD$,且$S_{\triangle ABC}=\frac{1}{2}BC\cdot AE$。
已知$AB = 6$,$CD = 3$,$AE = 4$。
由$\frac{1}{2}AB\cdot CD=\frac{1}{2}BC\cdot AE$可得:
$AB\cdot CD=BC\cdot AE$。
把$AB = 6$,$CD = 3$,$AE = 4$代入$AB\cdot CD=BC\cdot AE$中,得到$6×3 = 4× BC$。
则$BC=\frac{6×3}{4}=\frac{18}{4}=\frac{9}{2}$。
所以$BC$的长为$\frac{9}{2}$。
查看更多完整答案,请扫码查看


