1. 下图中,$\triangle ABC$的外角是 [教材P80定义变式](
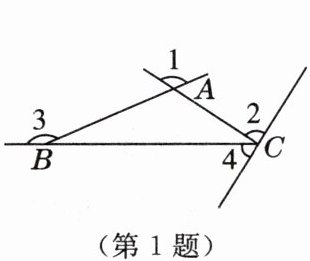
A.$\angle 1$
B.$\angle 2$
C.$\angle 3$
D.$\angle 4$
C
)
A.$\angle 1$
B.$\angle 2$
C.$\angle 3$
D.$\angle 4$
答案:
C
2. 如图,在$\triangle ABC$中,$D是BC$延长线上一点,$\angle B = 40^{\circ}$,$\angle ACD = 120^{\circ}$,则$\angle A$的度数是 [教材P82练习T1(1)变式1](
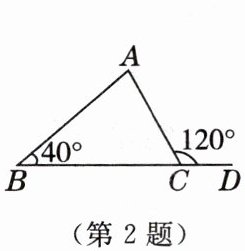
A.$80^{\circ}$
B.$60^{\circ}$
C.$160^{\circ}$
D.$100^{\circ}$
A
)
A.$80^{\circ}$
B.$60^{\circ}$
C.$160^{\circ}$
D.$100^{\circ}$
答案:
A
3. 如图,已知直线$a$,$b被直线c$,$d$所截,且$a// b$,$\angle 1 = 70^{\circ}$,$\angle 2 = 25^{\circ}$,则$\angle 3$的度数为 [教材P82练习T1(1)变式2](

A.$25^{\circ}$
B.$35^{\circ}$
C.$45^{\circ}$
D.$70^{\circ}$
C
)
A.$25^{\circ}$
B.$35^{\circ}$
C.$45^{\circ}$
D.$70^{\circ}$
答案:
C
4. 如图,在$\triangle ABC$中,$\angle B = 40^{\circ}$,$E是\triangle ABC$两外角平分线的交点,则$\angle AEC$的度数为
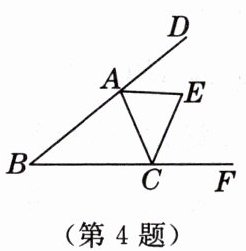
70°
. [教材P87复习题A组T5变式]
答案:
70°
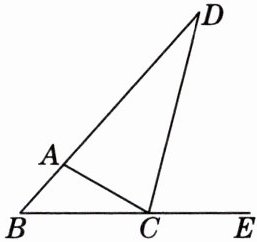
5. 如图,已知$CD是\triangle ABC的外角\angle ACE$的平分线,$CD交BA的延长线于点D$. [教材P82练习T2变式]
(1) 若$\angle ACE = 150^{\circ}$,$\angle BAC = 100^{\circ}$,求$\angle B$的度数;
(2) 请说明$\angle BAC > \angle B$.
(1) 若$\angle ACE = 150^{\circ}$,$\angle BAC = 100^{\circ}$,求$\angle B$的度数;
(2) 请说明$\angle BAC > \angle B$.

答案:
5.解:
(1)∠B=50°.
(2)
∵CD 是∠ACE 的平分线,
∴∠ACD=∠ECD.
∵∠BAC 是△ACD 的外角,
∴∠BAC>∠ACD,
∴∠BAC>∠ECD.
∵∠ECD 是△BCD 的外角,
∴∠ECD>∠B,
∴∠BAC>∠B.
(1)∠B=50°.
(2)
∵CD 是∠ACE 的平分线,
∴∠ACD=∠ECD.
∵∠BAC 是△ACD 的外角,
∴∠BAC>∠ACD,
∴∠BAC>∠ECD.
∵∠ECD 是△BCD 的外角,
∴∠ECD>∠B,
∴∠BAC>∠B.
查看更多完整答案,请扫码查看


