《2025年点拨训练八年级数学上册沪科版安徽专版》

1. “经过两点有一条直线,并且只有一条直线”属于 [教材 P76 概念变式 1] (C)
A.定义
B.定理
C.基本事实
D.以上答案都不对

答案： C

2. 下列语句中,是定义的是 [教材 P76 概念变式 2] (B)
A.两点确定一条直线
B.在同一平面内,不相交的两条直线叫作平行线
C.三角形的角平分线是一条线段
D.同角的余角相等

答案： B

3. 下列说法正确的是 [教材 P76 概念变式 3] (C)
A.命题是定理,定理是命题
B.命题不一定是定理,定理不一定是命题
C.真命题有可能是定理,假命题不可能是定理
D.定理可能是真命题,也可能是假命题

答案： C

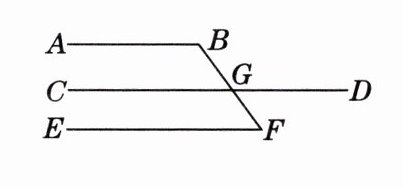
4. 推理填空：如图,直线 $ BF $ 与 $ CD $ 交于点 $ G $,已知 $ \angle B = \angle CGF $,$ \angle BGC = \angle F $. 求证：$ \angle B + \angle F = 180^{\circ} $,$ \angle F + \angle BGD = 180^{\circ} $. [教材 P77 练习 T2 变式]
证明：$ \because \angle B = \angle CGF $(已知),
$ \therefore AB // CD $(同位角相等,两直线平行).
$ \because \angle BGC = \angle F $(已知),
$ \therefore CD // EF $(同位角相等,两直线平行).
$ \therefore AB // EF $(平行公理的推论).
$ \therefore \angle B + \angle F = 180^{\circ} $(两直线平行,同旁内角互补).
又 $ \because \angle BGC + \angle BGD = 180^{\circ} $(平角的定义),
$ \angle BGC = \angle F $(已知),
$ \therefore \angle F + \angle BGD = 180^{\circ} $(等量代换).

答案： 同位角相等,两直线平行;同位角相等,两直线平行;平行公理的推论;两直线平行,同旁内角互补;平角的定义;等量代换