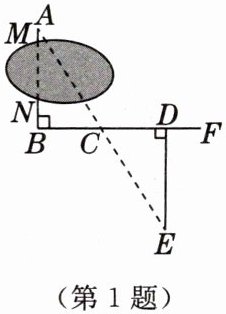
1. 如图,要测量池塘 $ M $,$ N $ 两点间的距离,可以在直线 $ MN $ 上取 $ A $,$ B $ 两点,再在池塘外取 $ AB $ 的垂线 $ BF $ 上的两点 $ C $,$ D $,使 $ BC = CD $,过点 $ D $ 再画出 $ BF $ 的垂线 $ DE $,使点 $ E $ 与点 $ A $,$ C $ 在一条直线上. 若此时测得 $ DE = 16 \, m $,$ AM = 0.5 \, m $,$ BN = 1.5 \, m $,则 $ M $,$ N $ 两点间的距离为
14
$ m $. [教材 P99 例 4 变式]
答案:
14
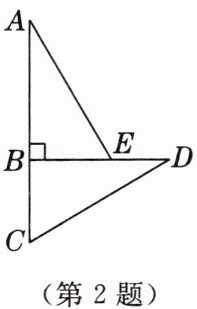
2. 如图,$ AC \perp BD $,垂足为 $ B $,$ E $ 为 $ BD $ 上一点,$ BC = BE $,$ \angle C = \angle AEB $,$ AB = 6 \, cm $,则图中长度为 $ 6 \, cm $ 的线段还有 ______
BD
. [教材 P110 习题 T3 变式]
答案:
BD
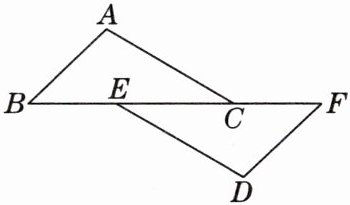
3. 如图,已知点 $ B $,$ E $,$ C $,$ F $ 在一条直线上,$ AC // DE $,$ AC = DE $,$ \angle A = \angle D $. [教材 P110 习题 T2 变式]
(1) 求证:$ AB = DF $;
(2) 若 $ BC = 9 $,$ EC = 5 $,求 $ BF $ 的长.
(1) 求证:$ AB = DF $;
(2) 若 $ BC = 9 $,$ EC = 5 $,求 $ BF $ 的长.

答案:
(1)证明:
∵AC//DE,
∴∠ACB=∠DEF.
在△ABC和△DFE中,
∵∠A=∠D,AC=DE,∠ACB=∠DEF,
∴△ABC≌△DFE(ASA),
∴AB=DF.
(2)解:BF=13.
(1)证明:
∵AC//DE,
∴∠ACB=∠DEF.
在△ABC和△DFE中,
∵∠A=∠D,AC=DE,∠ACB=∠DEF,
∴△ABC≌△DFE(ASA),
∴AB=DF.
(2)解:BF=13.
查看更多完整答案,请扫码查看


