1. 下列说法正确的是 [教材P92练习T1变式](
A.全等三角形是指形状、大小相同的三角形
B.两个全等三角形的面积不一定相等
C.周长相等的两个三角形是全等三角形
D.所有的等边三角形都是全等三角形
A
)A.全等三角形是指形状、大小相同的三角形
B.两个全等三角形的面积不一定相等
C.周长相等的两个三角形是全等三角形
D.所有的等边三角形都是全等三角形
答案:
A
2. 如图,△ABC与△BAD全等,∠C与∠D是对应角,AC与BD是对应边,这两个全等三角形可表示为
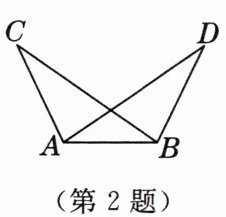
△ABC≌△BAD
,这两个全等三角形其余的对应角是∠CAB与∠DBA,∠ABC与∠BAD
,这两个全等三角形其余的对应边是AB与BA,BC与AD
.[教材P92练习T2变式]
答案:
△ABC≌△BAD;∠CAB与∠DBA,∠ABC与∠BAD;AB与BA,BC与AD
3. 如图,△ADE≌△BCF,点A,C,D,B共线,AD= 6 cm,CD= 5 cm,则BD=
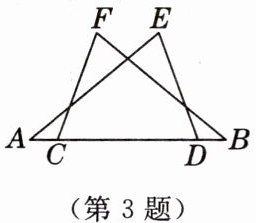
1
cm.[教材P93习题T3变式]
答案:
1
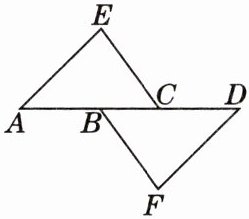
4. 如图,点A,B,C,D在同一直线上,△ACE≌△DBF,AD= 8,BC= 2.[教材P93习题T4变式]
(1)求AC的长;
(2)求证:CE//BF,AE//DF.
(1)求AC的长;
(2)求证:CE//BF,AE//DF.

答案:
1. (1)
解:
因为$\triangle ACE\cong\triangle DBF$,根据全等三角形的性质,全等三角形的对应边相等,所以$AC = DB$。
又因为$AC=AB + BC$,$DB = DC+BC$,所以$AB = DC$。
已知$AD = AB + BC+DC=8$,$BC = 2$,设$AB = DC=x$,则$x + 2+x=8$。
化简方程$2x+2 = 8$,移项可得$2x=8 - 2$,即$2x = 6$,解得$x = 3$。
那么$AC=AB + BC$,把$AB = 3$,$BC = 2$代入可得$AC=3 + 2=5$。
2. (2)
证明:
因为$\triangle ACE\cong\triangle DBF$,根据全等三角形的性质,全等三角形的对应角相等。
所以$\angle ECA=\angle FBD$,$\angle A=\angle D$。
根据内错角相等,两直线平行,由$\angle ECA=\angle FBD$,可得$CE// BF$;由$\angle A=\angle D$,可得$AE// DF$。
综上,(1)$AC$的长为$5$;(2)证明如上。
解:
因为$\triangle ACE\cong\triangle DBF$,根据全等三角形的性质,全等三角形的对应边相等,所以$AC = DB$。
又因为$AC=AB + BC$,$DB = DC+BC$,所以$AB = DC$。
已知$AD = AB + BC+DC=8$,$BC = 2$,设$AB = DC=x$,则$x + 2+x=8$。
化简方程$2x+2 = 8$,移项可得$2x=8 - 2$,即$2x = 6$,解得$x = 3$。
那么$AC=AB + BC$,把$AB = 3$,$BC = 2$代入可得$AC=3 + 2=5$。
2. (2)
证明:
因为$\triangle ACE\cong\triangle DBF$,根据全等三角形的性质,全等三角形的对应角相等。
所以$\angle ECA=\angle FBD$,$\angle A=\angle D$。
根据内错角相等,两直线平行,由$\angle ECA=\angle FBD$,可得$CE// BF$;由$\angle A=\angle D$,可得$AE// DF$。
综上,(1)$AC$的长为$5$;(2)证明如上。
查看更多完整答案,请扫码查看


