1. 如图,$AB = AC$,$DB = DC$,则直接由“$SSS$”可以判定(
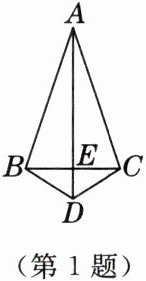
A.$\triangle ABD\cong\triangle ACD$
B.$\triangle ABE\cong\triangle ACE$
C.$\triangle EBD\cong\triangle ECD$
D.以上都不对
A
)
A.$\triangle ABD\cong\triangle ACD$
B.$\triangle ABE\cong\triangle ACE$
C.$\triangle EBD\cong\triangle ECD$
D.以上都不对
答案:
A
2. 如图是雨伞在开合过程中某时刻的截面示意图,伞骨$AB = AC$,$D$,$E分别是AB$,$AC$的中点,$DM$,$EM$是连接弹簧和伞骨的支架,且$DM = EM$.已知弹簧$M$在上下滑动的过程中,总有$\triangle ADM\cong\triangle AEM$,其判定依据是
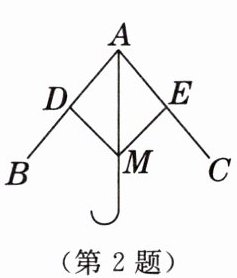
SSS
,雨伞的构造原理,利用了三角形的______稳定
性.
答案:
SSS;稳定
3. 如图,已知$AD = BC$,根据“$SSS$”,还需要一个条件:
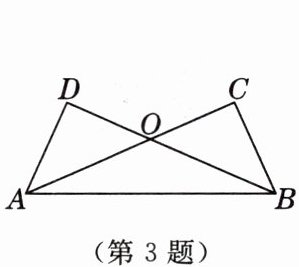
BD=AC
,可证明$\triangle ABC\cong\triangle BAD$.
答案:
BD=AC
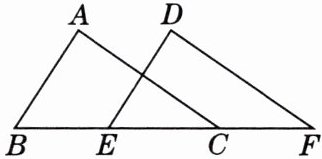
4. 如图,点$B$,$E$,$C$,$F$在同一条直线上,在$\triangle ABC和\triangle DEF$中,$BE = CF$,$AB = DE$,$AC = DF$.求证:
[教材P101例5变式]
(1)$\triangle ABC\cong\triangle DEF$;
(2)$AB// DE$.
[教材P101例5变式]
(1)$\triangle ABC\cong\triangle DEF$;
(2)$AB// DE$.

答案:
证明:
(1)
∵BE=CF,
∴BE+CE=CF+CE,即BC=EF.在△ABC和△DEF中,
∵{BC=EF,AB=DE,AC=DF,
∴△ABC≌△DEF(SSS).
(2)由
(1)知△ABC≌△DEF,
∴∠B=∠DEF.
∴AB//DE.
(1)
∵BE=CF,
∴BE+CE=CF+CE,即BC=EF.在△ABC和△DEF中,
∵{BC=EF,AB=DE,AC=DF,
∴△ABC≌△DEF(SSS).
(2)由
(1)知△ABC≌△DEF,
∴∠B=∠DEF.
∴AB//DE.
查看更多完整答案,请扫码查看


