1. 如图是一款折叠凳撑开时的侧面示意图(材料宽度忽略不计),其中凳腿 $ AB $ 和 $ CD $ 的长相等, $ O $ 是它们的中点. 为了使折叠凳坐着舒适,厂家将撑开时的凳面宽度 $ AD $ 设计为 $ 30 \, cm $,则撑开时的凳腿间距 $ CB $ 的长为
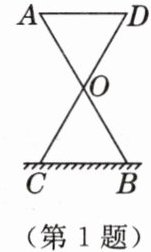
30
$ cm $. [教材 P97 练习 T2 变式]
答案:
30
2. 如图,点 $ B,E,C,F $ 在同一直线上,已知 $ \angle ABC = \angle DEF $, $ BE = CF $,要说明 $ \triangle ABC \cong \triangle DEF $,若以“ $ SAS $”为依据,还要添加的条件为
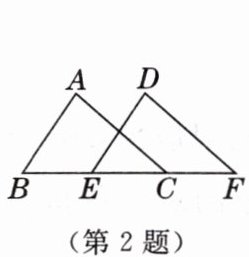
AB=DE
. [教材 P111 习题 T7 变式 1]
答案:
AB=DE
3. 如图,在 $ \triangle ABC $ 和 $ \triangle ADC $ 中, $ AB = AD $, $ \angle BAC = \angle DAC = 35^{\circ} $, $ \angle ADC = 100^{\circ} $,则 $ \angle ACB = $
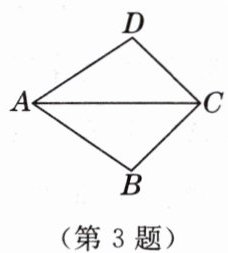
45
$ ^{\circ} $. [教材 P111 习题 T7 变式 2]
答案:
45
4. 如图,已知 $ AB \perp AC $, $ AD \perp AE $, $ AB = AC $, $ AD = AE $, $ BE $ 与 $ AC $, $ DC $ 分别交于点 $ G,F $. 求证: $ \angle BFD = 90^{\circ} $. [教材 P97 练习 T3 变式]
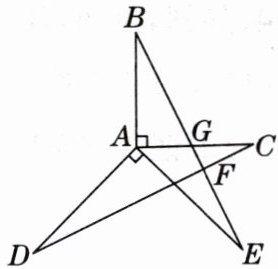

答案:
证明:
∵AB⊥AC,AD⊥AE(已知),
∴∠BAC=∠DAE=90°(垂直的定义)。
∴∠BAC+∠CAE=∠DAE+∠CAE(等式的性质),即∠BAE=∠CAD。
在△BAE和△CAD中,
$\left\{\begin{array}{l} AB=AC(已知)\\ ∠BAE=∠CAD(已证)\\ AE=AD(已知)\end{array}\right.$,
∴△BAE≌△CAD(SAS)。
∴∠ABE=∠ACD(全等三角形对应角相等)。
设∠ABE=∠ACD=α,
在△AGB中,∠BAC=90°,
∴∠AGB=180°-∠BAC-∠ABE=180°-90°-α=90°-α(三角形内角和定理)。
∵∠AGB=∠CGF(对顶角相等),
∴∠CGF=90°-α。
在△CGF中,∠GCF=α,
∴∠GFC=180°-∠CGF-∠GCF=180°-(90°-α)-α=90°(三角形内角和定理)。
∵∠GFC=∠BFD(对顶角相等),
∴∠BFD=90°。
综上,∠BFD=90°。
∵AB⊥AC,AD⊥AE(已知),
∴∠BAC=∠DAE=90°(垂直的定义)。
∴∠BAC+∠CAE=∠DAE+∠CAE(等式的性质),即∠BAE=∠CAD。
在△BAE和△CAD中,
$\left\{\begin{array}{l} AB=AC(已知)\\ ∠BAE=∠CAD(已证)\\ AE=AD(已知)\end{array}\right.$,
∴△BAE≌△CAD(SAS)。
∴∠ABE=∠ACD(全等三角形对应角相等)。
设∠ABE=∠ACD=α,
在△AGB中,∠BAC=90°,
∴∠AGB=180°-∠BAC-∠ABE=180°-90°-α=90°-α(三角形内角和定理)。
∵∠AGB=∠CGF(对顶角相等),
∴∠CGF=90°-α。
在△CGF中,∠GCF=α,
∴∠GFC=180°-∠CGF-∠GCF=180°-(90°-α)-α=90°(三角形内角和定理)。
∵∠GFC=∠BFD(对顶角相等),
∴∠BFD=90°。
综上,∠BFD=90°。
查看更多完整答案,请扫码查看


