2025年新课堂假期生活暑假用书五年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新课堂假期生活暑假用书五年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
填三边
画一个三角形,在它的三个顶点和三边的中点各画一个小圆圈。然后把1,2,3,4,5,6分别填写到这6个小圆圈里,使三角形每条边上3个数的和都相等。
通过尝试,容易得到满足要求的填法,而且不止一种。例如可以填成下图中的两种情况:在左图中,每一边上3个数的和都是11;在右图中,每一边上3个数的和都是10。
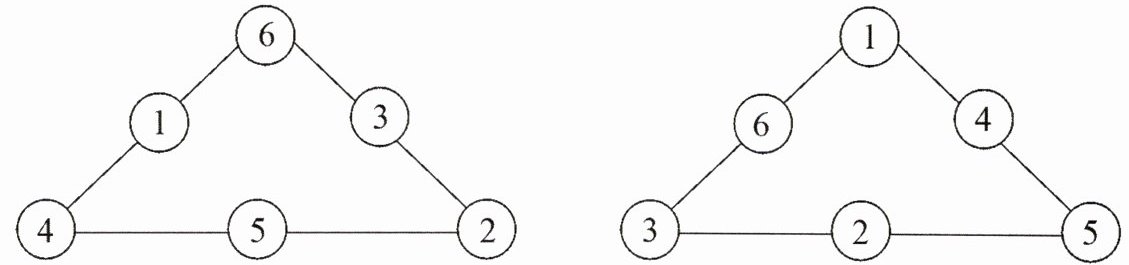
能不能找到一种填法,使各边上3个数的和不但相等,而且达到最大,然后再达到最小?
画一个三角形,在它的三个顶点和三边的中点各画一个小圆圈。然后把1,2,3,4,5,6分别填写到这6个小圆圈里,使三角形每条边上3个数的和都相等。
通过尝试,容易得到满足要求的填法,而且不止一种。例如可以填成下图中的两种情况:在左图中,每一边上3个数的和都是11;在右图中,每一边上3个数的和都是10。

能不能找到一种填法,使各边上3个数的和不但相等,而且达到最大,然后再达到最小?
答案:
解析:本题主要考查加法运算。
观察发现三角形每条边上3个数的和要相等,而且要使和达到最大或者最小,需要分析数字的组合方式。
要使每条边上3个数的和最大,那么应该让较大的数尽量多次被使用。
要使每条边上3个数的和最小,那么应该让较小的数尽量多次被使用。
先求最大情况:
六个数的总和为$1 + 2 + 3 + 4 + 5 + 6 = 21$。
设每条边上的和为$S$,三个顶点的数分别为$a$,$b$,$c$,三边中点分别为$d$,$e$,$f$。
则$S=a + d + b=b + e + c=c + f + a$,
$3S=(a + b + c)+(d + e + f)+(a + b + c)=21+(a + b + c)$。
要使$S$最大,也就是$a + b + c$最大,因为$a$,$b$,$c$是顶点数,会被重复计算一次。
当$a + b + c = 6 + 5 + 4 = 15$时(取最大的三个数作为顶点数),
$3S=21 + 15=36$,$S = 12$。
一种可能的填法是:顶点依次填$4$,$5$,$6$,三边中点依次填$2$,$1$,$3$(答案不唯一,只要满足每条边和为$12$即可)。
再求最小情况:
要使$S$最小,也就是$a + b + c$最小。
当$a + b + c=1 + 2 + 3 = 6$时(取最小的三个数作为顶点数),
$3S=21 + 6=27$,$S = 9$。
一种可能的填法是:顶点依次填$1$,$2$,$3$,三边中点依次填$5$,$4$,$6$(答案不唯一,只要满足每条边和为$9$即可)。
答案:最大情况:每条边上3个数的和最大是$12$(填法不唯一,如顶点依次填$4$,$5$,$6$,三边中点依次填$2$,$1$,$3$ )。
最小情况:每条边上3个数的和最小是$9$(填法不唯一,如顶点依次填$1$,$2$,$3$,三边中点依次填$5$,$4$,$6$ )。
观察发现三角形每条边上3个数的和要相等,而且要使和达到最大或者最小,需要分析数字的组合方式。
要使每条边上3个数的和最大,那么应该让较大的数尽量多次被使用。
要使每条边上3个数的和最小,那么应该让较小的数尽量多次被使用。
先求最大情况:
六个数的总和为$1 + 2 + 3 + 4 + 5 + 6 = 21$。
设每条边上的和为$S$,三个顶点的数分别为$a$,$b$,$c$,三边中点分别为$d$,$e$,$f$。
则$S=a + d + b=b + e + c=c + f + a$,
$3S=(a + b + c)+(d + e + f)+(a + b + c)=21+(a + b + c)$。
要使$S$最大,也就是$a + b + c$最大,因为$a$,$b$,$c$是顶点数,会被重复计算一次。
当$a + b + c = 6 + 5 + 4 = 15$时(取最大的三个数作为顶点数),
$3S=21 + 15=36$,$S = 12$。
一种可能的填法是:顶点依次填$4$,$5$,$6$,三边中点依次填$2$,$1$,$3$(答案不唯一,只要满足每条边和为$12$即可)。
再求最小情况:
要使$S$最小,也就是$a + b + c$最小。
当$a + b + c=1 + 2 + 3 = 6$时(取最小的三个数作为顶点数),
$3S=21 + 6=27$,$S = 9$。
一种可能的填法是:顶点依次填$1$,$2$,$3$,三边中点依次填$5$,$4$,$6$(答案不唯一,只要满足每条边和为$9$即可)。
答案:最大情况:每条边上3个数的和最大是$12$(填法不唯一,如顶点依次填$4$,$5$,$6$,三边中点依次填$2$,$1$,$3$ )。
最小情况:每条边上3个数的和最小是$9$(填法不唯一,如顶点依次填$1$,$2$,$3$,三边中点依次填$5$,$4$,$6$ )。
查看更多完整答案,请扫码查看


