2025年新课堂假期生活暑假用书五年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新课堂假期生活暑假用书五年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 1桶矿泉水的容积约是5
升
一杯酸奶的容积约是250毫升
答案:
解析:题目考查的是容积的单位。在中文语境中,描述液体容积时,常用的单位有“升”和“毫升”。对于较大的容积,一般使用“升”作为单位;对于较小的容积,则使用“毫升”作为单位。
一桶矿泉水的容积较大,所以应该使用“升”作为单位;
一杯酸奶的容积较小,所以应该使用“毫升”作为单位。
答案:1. 升;毫升。
一桶矿泉水的容积较大,所以应该使用“升”作为单位;
一杯酸奶的容积较小,所以应该使用“毫升”作为单位。
答案:1. 升;毫升。
2. $ 3×( )= \frac {2}{7}×( )= \frac {4}{5}÷( )= 0.25×( )= 1 $
答案:
解析:
题目考查的是数学中的等式求解以及分数、小数和整数的运算。
需要找到一个数,使得$3$乘以这个数等于$1$,同样,需要找到一个数,使得$\frac{2}{7}$乘以这个数等于$1$,以此类推。
这实际上是在求各个数的倒数或者通过除法来找到缺失的数。
对于整数和小数的组合,可以通过除法直接求得答案;
对于分数,需要找到其倒数来使得乘积为$1$。
答案:
$3 × \frac{1}{3} = 1$,所以第一个空填$\frac{1}{3}$;
$\frac{2}{7} × \frac{7}{2} = 1$,所以第二个空填$\frac{7}{2}$,也可以写成$3.5$;
$\frac{4}{5} ÷ 1 = \frac{4}{5}$,而$\frac{4}{5} × \frac{5}{4} = 1$,所以第三个空应该填$\frac{5}{4}$,也可以写成$1.25$,但考虑到题目中的形式,我们填$\frac{5}{4}$;
$0.25 × 4 = 1$,所以第四个空填$4$;
所以,$3 × (\frac{1}{3}) = \frac{2}{7} × (\frac{7}{2}) = \frac{4}{5} ÷ (\frac{5}{4}) = 0.25 × (4) = 1$。
题目考查的是数学中的等式求解以及分数、小数和整数的运算。
需要找到一个数,使得$3$乘以这个数等于$1$,同样,需要找到一个数,使得$\frac{2}{7}$乘以这个数等于$1$,以此类推。
这实际上是在求各个数的倒数或者通过除法来找到缺失的数。
对于整数和小数的组合,可以通过除法直接求得答案;
对于分数,需要找到其倒数来使得乘积为$1$。
答案:
$3 × \frac{1}{3} = 1$,所以第一个空填$\frac{1}{3}$;
$\frac{2}{7} × \frac{7}{2} = 1$,所以第二个空填$\frac{7}{2}$,也可以写成$3.5$;
$\frac{4}{5} ÷ 1 = \frac{4}{5}$,而$\frac{4}{5} × \frac{5}{4} = 1$,所以第三个空应该填$\frac{5}{4}$,也可以写成$1.25$,但考虑到题目中的形式,我们填$\frac{5}{4}$;
$0.25 × 4 = 1$,所以第四个空填$4$;
所以,$3 × (\frac{1}{3}) = \frac{2}{7} × (\frac{7}{2}) = \frac{4}{5} ÷ (\frac{5}{4}) = 0.25 × (4) = 1$。
3. 把一个长6cm,宽5cm,高4cm的长方体截成一个最大的正方体,则这个正方体的体积是(
64
)$ cm^{3} $。
答案:
解析:本题主要考查正方体的特征及体积计算。
要从一个长$6cm$,宽$5cm$,高$4cm$的长方体中截出一个最大的正方体,需要找出长、宽、高的最小值,因为正方体的所有棱长都是相等的。
在这个长方体中,长、宽、高的最小值是$4cm$,所以截出的最大正方体的棱长也是$4cm$。
正方体的体积计算公式是:
体积$= $棱长$^{3}$
将棱长$4cm$代入公式,得到:
体积$= 4^{3} = 64(cm^{3})$。
答案:$64$。
要从一个长$6cm$,宽$5cm$,高$4cm$的长方体中截出一个最大的正方体,需要找出长、宽、高的最小值,因为正方体的所有棱长都是相等的。
在这个长方体中,长、宽、高的最小值是$4cm$,所以截出的最大正方体的棱长也是$4cm$。
正方体的体积计算公式是:
体积$= $棱长$^{3}$
将棱长$4cm$代入公式,得到:
体积$= 4^{3} = 64(cm^{3})$。
答案:$64$。
4. 一辆货车$ \frac {2}{5} $小时行驶22km,平均每小时行驶(
55
)km,行驶1km需要($\frac{1}{55}$
)小时。
答案:
解析:
本题考查速度、时间和路程的关系。
首先,计算货车的平均速度。
平均速度 $v$ 的公式是:
$v = \frac{\text{总路程}}{\text{总时间}}$。
根据题目,货车在 $\frac{2}{5}$ 小时内行驶了 22 km,所以平均速度为:
$v = \frac{22}{\frac{2}{5}} = 22 × \frac{5}{2} = 55 \text{(km/h)}$。
接下来,计算货车行驶 1 km 所需的时间。
时间 $t$ 的公式是:
$t = \frac{\text{路程}}{\text{速度}}$。
所以行驶 1 km 所需的时间为:
$t = \frac{1}{55} \text{(小时)}$。
答案:
平均每小时行驶 55 km;
行驶 1 km 需要 $\frac{1}{55}$ 小时。
本题考查速度、时间和路程的关系。
首先,计算货车的平均速度。
平均速度 $v$ 的公式是:
$v = \frac{\text{总路程}}{\text{总时间}}$。
根据题目,货车在 $\frac{2}{5}$ 小时内行驶了 22 km,所以平均速度为:
$v = \frac{22}{\frac{2}{5}} = 22 × \frac{5}{2} = 55 \text{(km/h)}$。
接下来,计算货车行驶 1 km 所需的时间。
时间 $t$ 的公式是:
$t = \frac{\text{路程}}{\text{速度}}$。
所以行驶 1 km 所需的时间为:
$t = \frac{1}{55} \text{(小时)}$。
答案:
平均每小时行驶 55 km;
行驶 1 km 需要 $\frac{1}{55}$ 小时。
5. 一个正方体的棱长是6cm,它的棱长和是(
72
)cm,表面积是(216
)$ cm^{2} $,体积是(216
)$ cm^{3} $。
答案:
解析:本题主要考查正方体的棱长和、表面积和体积的计算。
正方体有12条棱,每条棱的长度相等,所以棱长和是棱长乘以12。
正方体的表面积是6个面的面积之和,每个面的面积是棱长的平方。
正方体的体积是棱长的三次方。
答案:
棱长和:$6 × 12 = 72(cm)$;
表面积:$6 × 6 × 6 = 216(cm^{2})$;
体积:$6 × 6 × 6 = 216(cm^{3})$。
所以,它的棱长和是72cm,表面积是$216cm^{2}$,体积是$216cm^{3}$。
正方体有12条棱,每条棱的长度相等,所以棱长和是棱长乘以12。
正方体的表面积是6个面的面积之和,每个面的面积是棱长的平方。
正方体的体积是棱长的三次方。
答案:
棱长和:$6 × 12 = 72(cm)$;
表面积:$6 × 6 × 6 = 216(cm^{2})$;
体积:$6 × 6 × 6 = 216(cm^{3})$。
所以,它的棱长和是72cm,表面积是$216cm^{2}$,体积是$216cm^{3}$。
二、看图填一填。
下图是小明站在自己家观测到几个建筑物的平面图。以小明家为观测点:
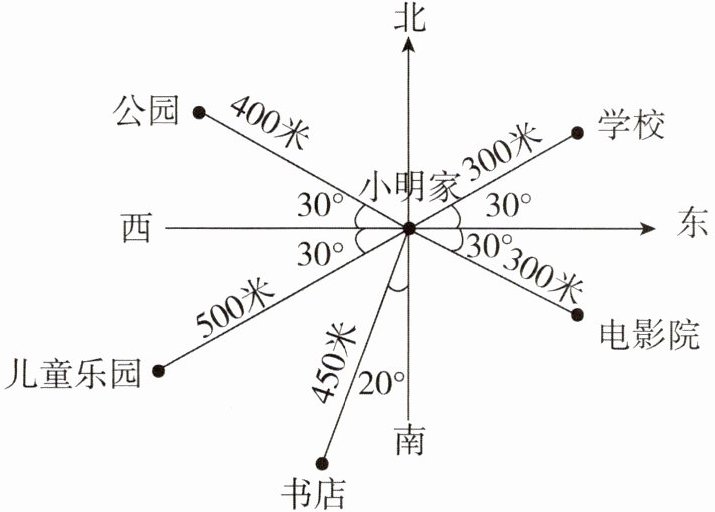
(1)学校的位置在(
(2)电影院的位置在(
(3)书店的位置在(
(4)儿童乐园的位置在(
(5)公园的位置在(
下图是小明站在自己家观测到几个建筑物的平面图。以小明家为观测点:

(1)学校的位置在(
东
)偏(北
)(30°
)的方向上,离小明家(300
)米。(2)电影院的位置在(
东
)偏(南
)(30°
)的方向上,离小明家(300
)米。(3)书店的位置在(
南
)偏(西
)(20°
)的方向上,离小明家(450
)米。(4)儿童乐园的位置在(
西
)偏(南
)(30°
)的方向上,离小明家(500
)米。(5)公园的位置在(
西
)偏(北
)(30°
)的方向上,离小明家(400
)米。
答案:
(1)东 北 30° 300
(2)东 南 30° 300
(3)南 西 20° 450
(4)西 南 30° 500
(5)西 北 30° 400
(1)东 北 30° 300
(2)东 南 30° 300
(3)南 西 20° 450
(4)西 南 30° 500
(5)西 北 30° 400
查看更多完整答案,请扫码查看


