2025年暑假作业南方出版社五年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业南方出版社五年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
一、看谁先到家。
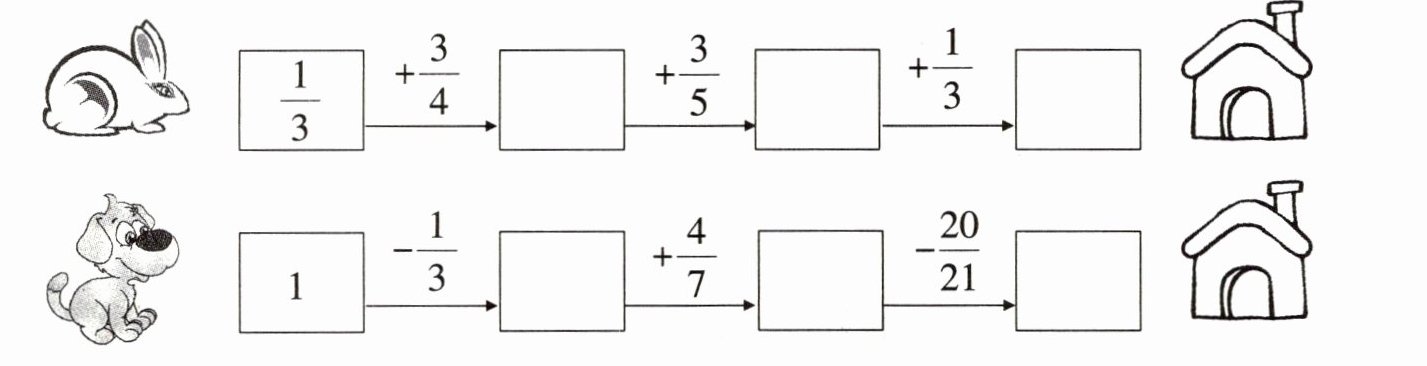

答案:
兔子的序列:
- \(\frac{1}{3}\)
- \(\frac{13}{12}\)
- \(\frac{101}{60}\)
- \(\frac{121}{60}\)
狗的序列:
- 1
- \(\frac{2}{3}\)
- \(\frac{26}{21}\)
- \(\frac{2}{7}\)
二、在 里填上合适的分数。
里填上合适的分数。
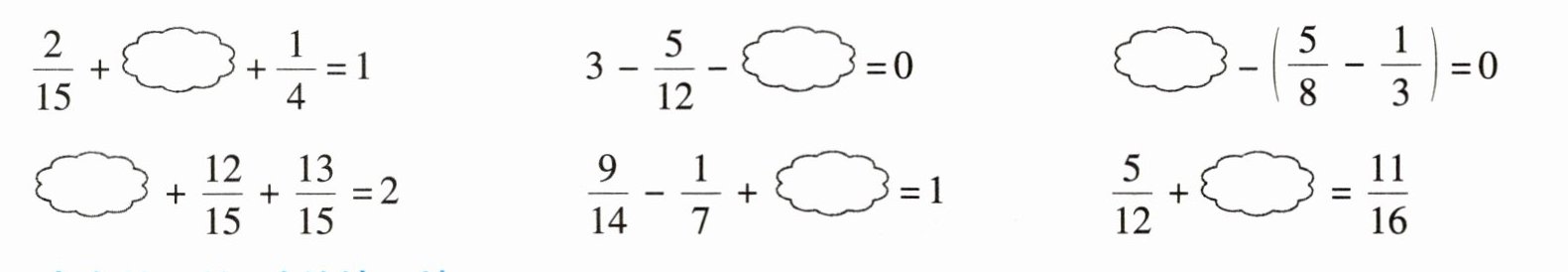
 里填上合适的分数。
里填上合适的分数。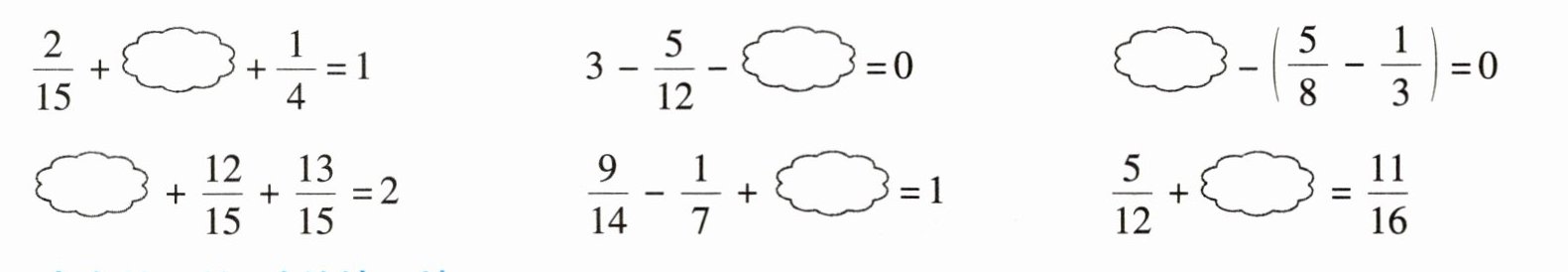
答案:
$\frac{37}{60}$,$\frac{31}{12}$,$\frac{7}{24}$,$\frac{1}{3}$,$\frac{1}{2}$,$\frac{13}{48}$
三、亲自练一练,动笔填一填。
1. 既是 84 的因数,又是 6 的倍数的数有( )。
2. 一个数既是 12 的倍数,又是 288 的因数,这个数可能是( )。
3. 对于 72 ,
, 中填( )或( )时,既是 2 的倍数,又是 3 的倍数;
中填( )或( )时,既是 2 的倍数,又是 3 的倍数; 中填( )时,既是 3 的倍数,又是 5 的倍数。
中填( )时,既是 3 的倍数,又是 5 的倍数。
1. 既是 84 的因数,又是 6 的倍数的数有( )。
2. 一个数既是 12 的倍数,又是 288 的因数,这个数可能是( )。
3. 对于 72
 ,
, 中填( )或( )时,既是 2 的倍数,又是 3 的倍数;
中填( )或( )时,既是 2 的倍数,又是 3 的倍数; 中填( )时,既是 3 的倍数,又是 5 的倍数。
中填( )时,既是 3 的倍数,又是 5 的倍数。
答案:
1. $6$、$12$、$42$、$84$
2. $12$、$24$、$36$、$48$、$72$、$144$、$288$
3. $0$、$6$;$0$
2. $12$、$24$、$36$、$48$、$72$、$144$、$288$
3. $0$、$6$;$0$
四、求下面每组数的最大公因数和最小公倍数。
30 和 45 25 和 125 36 和 42 48 和 64
30 和 45 25 和 125 36 和 42 48 和 64
答案:
【解析】:
1. 求$30$和$45$的最大公因数和最小公倍数:
先对$30$和$45$分解质因数,$30 = 2\times3\times5$,$45=3\times3\times5$。
最大公因数是两个数公有质因数的乘积,$30$和$45$公有的质因数是$3$和$5$,所以它们的最大公因数$GCF(30,45)=3\times5 = 15$。
最小公倍数是两个数公有质因数与每个数独有质因数的连乘积,$30$独有的质因数是$2$,$45$独有的质因数是$3$,所以它们的最小公倍数$LCM(30,45)=2\times3\times3\times5=90$。
2. 求$25$和$125$的最大公因数和最小公倍数:
因为$125\div25 = 5$,即$125$是$25$的倍数。
当两个数为倍数关系时,最大公因数是较小的数,所以$GCF(25,125)=25$;最小公倍数是较大的数,所以$LCM(25,125)=125$。
3. 求$36$和$42$的最大公因数和最小公倍数:
对$36$和$42$分解质因数,$36 = 2\times2\times3\times3$,$42=2\times3\times7$。
它们公有的质因数是$2$和$3$,所以最大公因数$GCF(36,42)=2\times3 = 6$。
最小公倍数$LCM(36,42)=2\times2\times3\times3\times7 = 252$。
4. 求$48$和$64$的最大公因数和最小公倍数:
分解质因数,$48=2\times2\times2\times2\times3$,$64 = 2\times2\times2\times2\times2\times2$。
公有的质因数是$2\times2\times2\times2$,所以最大公因数$GCF(48,64)=2\times2\times2\times2=16$。
最小公倍数$LCM(48,64)=2\times2\times2\times2\times2\times2\times3=192$。
【答案】:
$30$和$45$的最大公因数是$15$,最小公倍数是$90$;
$25$和$125$的最大公因数是$25$,最小公倍数是$125$;
$36$和$42$的最大公因数是$6$,最小公倍数是$252$;
$48$和$64$的最大公因数是$16$,最小公倍数是$192$。
1. 求$30$和$45$的最大公因数和最小公倍数:
先对$30$和$45$分解质因数,$30 = 2\times3\times5$,$45=3\times3\times5$。
最大公因数是两个数公有质因数的乘积,$30$和$45$公有的质因数是$3$和$5$,所以它们的最大公因数$GCF(30,45)=3\times5 = 15$。
最小公倍数是两个数公有质因数与每个数独有质因数的连乘积,$30$独有的质因数是$2$,$45$独有的质因数是$3$,所以它们的最小公倍数$LCM(30,45)=2\times3\times3\times5=90$。
2. 求$25$和$125$的最大公因数和最小公倍数:
因为$125\div25 = 5$,即$125$是$25$的倍数。
当两个数为倍数关系时,最大公因数是较小的数,所以$GCF(25,125)=25$;最小公倍数是较大的数,所以$LCM(25,125)=125$。
3. 求$36$和$42$的最大公因数和最小公倍数:
对$36$和$42$分解质因数,$36 = 2\times2\times3\times3$,$42=2\times3\times7$。
它们公有的质因数是$2$和$3$,所以最大公因数$GCF(36,42)=2\times3 = 6$。
最小公倍数$LCM(36,42)=2\times2\times3\times3\times7 = 252$。
4. 求$48$和$64$的最大公因数和最小公倍数:
分解质因数,$48=2\times2\times2\times2\times3$,$64 = 2\times2\times2\times2\times2\times2$。
公有的质因数是$2\times2\times2\times2$,所以最大公因数$GCF(48,64)=2\times2\times2\times2=16$。
最小公倍数$LCM(48,64)=2\times2\times2\times2\times2\times2\times3=192$。
【答案】:
$30$和$45$的最大公因数是$15$,最小公倍数是$90$;
$25$和$125$的最大公因数是$25$,最小公倍数是$125$;
$36$和$42$的最大公因数是$6$,最小公倍数是$252$;
$48$和$64$的最大公因数是$16$,最小公倍数是$192$。
五、解方程。
$ x - 1.2 5 = \frac { 3 } { 4 } $$ $$ x + \frac { 7 } { 1 2 } = \frac { 7 } { 8 } $$ $$ 1 - x = \frac { 7 } { 1 1 } $
$ x - 1.2 5 = \frac { 3 } { 4 } $$ $$ x + \frac { 7 } { 1 2 } = \frac { 7 } { 8 } $$ $$ 1 - x = \frac { 7 } { 1 1 } $
答案:
【解析】:
1. 对于方程$x - 1.25=\frac{3}{4}$:
先将$1.25$转化为分数,$1.25 = \frac{5}{4}$,则原方程变为$x-\frac{5}{4}=\frac{3}{4}$。
根据等式的性质,等式两边同时加上$\frac{5}{4}$,得到$x-\frac{5}{4}+\frac{5}{4}=\frac{3}{4}+\frac{5}{4}$。
计算右边$\frac{3 + 5}{4}=\frac{8}{4}=2$,所以$x = 2$。
2. 对于方程$x+\frac{7}{12}=\frac{7}{8}$:
根据等式的性质,等式两边同时减去$\frac{7}{12}$,得到$x+\frac{7}{12}-\frac{7}{12}=\frac{7}{8}-\frac{7}{12}$。
先通分,$8$和$12$的最小公倍数是$24$,则$\frac{7}{8}-\frac{7}{12}=\frac{7\times3}{8\times3}-\frac{7\times2}{12\times2}=\frac{21}{24}-\frac{14}{24}$。
计算右边$\frac{21 - 14}{24}=\frac{7}{24}$,所以$x=\frac{7}{24}$。
3. 对于方程$1 - x=\frac{7}{11}$:
根据等式的性质,等式两边同时加上$x$,得到$1 - x+x=\frac{7}{11}+x$,即$1=\frac{7}{11}+x$。
再根据等式的性质,等式两边同时减去$\frac{7}{11}$,得到$1-\frac{7}{11}=\frac{7}{11}+x-\frac{7}{11}$。
计算左边$1-\frac{7}{11}=\frac{11}{11}-\frac{7}{11}=\frac{4}{11}$,所以$x=\frac{4}{11}$。
【答案】:$x = 2$;$x=\frac{7}{24}$;$x=\frac{4}{11}$
1. 对于方程$x - 1.25=\frac{3}{4}$:
先将$1.25$转化为分数,$1.25 = \frac{5}{4}$,则原方程变为$x-\frac{5}{4}=\frac{3}{4}$。
根据等式的性质,等式两边同时加上$\frac{5}{4}$,得到$x-\frac{5}{4}+\frac{5}{4}=\frac{3}{4}+\frac{5}{4}$。
计算右边$\frac{3 + 5}{4}=\frac{8}{4}=2$,所以$x = 2$。
2. 对于方程$x+\frac{7}{12}=\frac{7}{8}$:
根据等式的性质,等式两边同时减去$\frac{7}{12}$,得到$x+\frac{7}{12}-\frac{7}{12}=\frac{7}{8}-\frac{7}{12}$。
先通分,$8$和$12$的最小公倍数是$24$,则$\frac{7}{8}-\frac{7}{12}=\frac{7\times3}{8\times3}-\frac{7\times2}{12\times2}=\frac{21}{24}-\frac{14}{24}$。
计算右边$\frac{21 - 14}{24}=\frac{7}{24}$,所以$x=\frac{7}{24}$。
3. 对于方程$1 - x=\frac{7}{11}$:
根据等式的性质,等式两边同时加上$x$,得到$1 - x+x=\frac{7}{11}+x$,即$1=\frac{7}{11}+x$。
再根据等式的性质,等式两边同时减去$\frac{7}{11}$,得到$1-\frac{7}{11}=\frac{7}{11}+x-\frac{7}{11}$。
计算左边$1-\frac{7}{11}=\frac{11}{11}-\frac{7}{11}=\frac{4}{11}$,所以$x=\frac{4}{11}$。
【答案】:$x = 2$;$x=\frac{7}{24}$;$x=\frac{4}{11}$
查看更多完整答案,请扫码查看


