《2025年暑假作业假期园地七年级数学北师大版中原农民出版社》

12. $[(3x+4y)^{2}-3x(3x+4y)]÷(-6y)$,其中$x= -1,y= 3$.

答案： 原式 $ = ( 9 x ^ { 2 } + 24 x y + 16 y ^ { 2 } - 9 x ^ { 2 } - 12 x y ) \times ( - \frac { 1 } { 6 y } ) - \frac { 12 x y } { 6 y } - \frac { 16 y ^ { 2 } } { 6 y } = - 2 x - \frac { 8 } { 3 } y $，当 $ x = - 1 $，$ y = 3 $ 时，原式 $ = - 2 \times ( - 1 ) - \frac { 8 } { 3 } \times 3 = - 6 $

13. 已知$(a+2)^{2}+|a+b+5|= 0$,求$3a^{2}b-[2a^{2}b-(2ab-a^{2}b)-4a^{2}]-ab$的值.

答案： $ \because ( a + 2 ) ^ { 2 } \geq 0 $，$ | a + b + 5 | \geq 0 $，由 $ ( a + 2 ) ^ { 2 } + | a + b + 5 | = 0 $，得 $ a + 2 = 0 $，$ a + b + 5 = 0 $，解得 $ a = - 2 $，$ b = - 3 $。原式化简得 $ a b + 4 a ^ { 2 } $，值为 22。

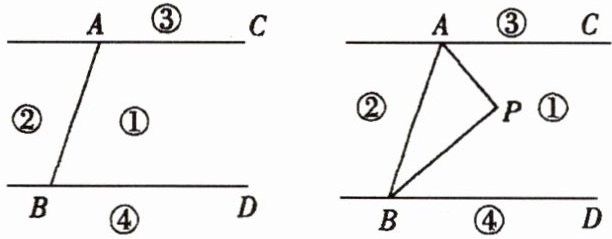
14. 如下图,直线$AC// BD$,连接AB,直线AC,BD及线段AB把平面分成①,②,③,④四个部分,规定：线上各点不属于任何部分.当动点P落在某个部位时,连接PA,PB构成$∠PAC,∠APB,∠PBD$三个角.(提示：有公共端点的两条重合的射线所组成的角是$0^{\circ }$角)当动点P落在第①部分时,试说明：$∠APB= ∠PAC+∠PBD$.

答案： 过点$P$作$PE// AC$，因为$AC// BD$，所以$PE// BD$。
由$PE// AC$得$\angle PAC = \angle APE$，由$PE// BD$得$\angle PBD=\angle BPE$。
因为$\angle APB=\angle APE+\angle BPE$，所以$\angle APB=\angle PAC + \angle PBD$。