《2025年暑假作业假期园地七年级数学北师大版中原农民出版社》

8. 已知：$a^{2}+4a - 1 = 0$,求$2a^{3}+11a^{2}+10a - 2017$的值.

答案： 解：
∵ $ a^{2} + 4a - 1 = 0 $，
∴ $ a^{2} + 4a = 1 $。
∴ $ 2a^{3} + 11a^{2} + 10a - 2017 = 2a^{3} + 8a^{2} + 3a^{2} + 12a - 2a - 2017 = 2a(a^{2} + 4a) + 3(a^{2} + 4a) - 2a - 2017 = 2a×1 + 3×1 - 2a - 2017 = -2014 $。

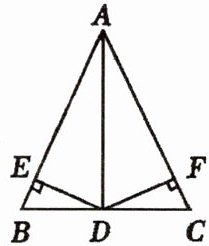
9. 在$\triangle ABC$中,$D是BC$的中点,$DE⊥AB$,$DF⊥AC$,垂足分别是点$E$、$F$,$BE = CF$.
(1)图中有几对全等三角形？请一一列出.
(2)选择一对你认为全等的三角形进行说明.

答案： 解：
(1) 中有 3 对全等三角形，分别是 $ △ABD ≌ △ACD $； $ △ADE ≌ △ADF $； $ △BDE ≌ △CDF $。
(2) 选择证明 $ △BDE ≌ △CDF $，证明：
∵ $ DE⊥AB $， $ DF⊥AC $，
∴ $ ∠BED = ∠CFD = 90° $。又
∵ D 是 BC 的中点，
∴ $ BD = CD $，在 $ Rt△BDE $ 和 $ Rt△CDF $ 中 $ \begin{cases} BD = CD \\ BE = CF \end{cases} $，
∴ $ △BDE ≌ △CDF $。

10. 一件由黄金和白银制成的首饰重$a$g,商家称其中黄金含量不低于$90\%$,黄金与白银的密度分别是$19.3g/cm^{3}与10.5g/cm^{3}$,列出不等式(组)表示这种首饰的体积应满足什么条件？(只列式子即可)(提示：质量$=密度×$体积)

答案： 设首饰中黄金的质量为$x$g，首饰体积为$Vcm^{3}$，则$V=\frac{x}{19.3}+\frac{a - x}{10.5}$，且$x\geqslant0.9a$，所以$\frac{0.9a}{19.3}+\frac{a - 0.9a}{10.5}\leqslant V\leqslant\frac{a}{19.3}$ 。