10. 已知 $ \triangle A B C $ 的三边长均为整数,$ \triangle A B C $ 的周长为奇数。
(1)若 $ A C = 8 $,$ B C = 2 $,求 $ A B $ 的长;
(2)若 $ A C - B C = 5 $,求 $ A B $ 的最小值。
(1)若 $ A C = 8 $,$ B C = 2 $,求 $ A B $ 的长;
7或9
(2)若 $ A C - B C = 5 $,求 $ A B $ 的最小值。
6
答案:
【解析】
(1)
∵ 由三角形的三边关系知,$AC - BC < AB < AC + BC$,即:$8 - 2 < AB < 8 + 2$,
∴ $6 < AB < 10$,又
∵ $\triangle ABC$ 的周长为奇数,而 $AC$、$BC$ 为偶数,
∴ $AB$ 为奇数,
∴ $AB = 7$ 或 9.
(2)
∵ $AC - BC = 5$,
∴ $AC$、$BC$ 中一个奇数、一个偶数,又
∵ $\triangle ABC$ 的周长为奇数,故 $AB$ 为偶数,
∴ $AB > AC - BC = 5$,得 $AB$ 的最小值为 6.
(1)
∵ 由三角形的三边关系知,$AC - BC < AB < AC + BC$,即:$8 - 2 < AB < 8 + 2$,
∴ $6 < AB < 10$,又
∵ $\triangle ABC$ 的周长为奇数,而 $AC$、$BC$ 为偶数,
∴ $AB$ 为奇数,
∴ $AB = 7$ 或 9.
(2)
∵ $AC - BC = 5$,
∴ $AC$、$BC$ 中一个奇数、一个偶数,又
∵ $\triangle ABC$ 的周长为奇数,故 $AB$ 为偶数,
∴ $AB > AC - BC = 5$,得 $AB$ 的最小值为 6.
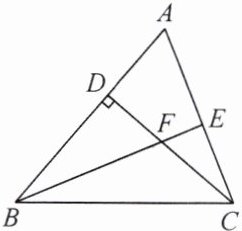
11. 如图,在 $ \triangle A B C $ 中,$ C D $ 是 $ A B $ 边上高,$ B E $ 为角平分线,若 $ \angle B F C = 110 ^ { \circ } $,求 $ \angle B C F $ 的度数。

50°
答案:
【解析】
∵ $CD$ 是 $AB$ 边上高,
∴ $\angle BDC = 90^{\circ}$,
∵ $\angle BFC = 110^{\circ}$,
∴ $\angle DBF = \angle BFC - \angle BDC = 20^{\circ}$,
∵ $BE$ 为角平分线,
∴ $\angle ABC = 2\angle DBF = 40^{\circ}$,
∴ $\angle BCF = 90^{\circ} - \angle ABC = 50^{\circ}$.
∵ $CD$ 是 $AB$ 边上高,
∴ $\angle BDC = 90^{\circ}$,
∵ $\angle BFC = 110^{\circ}$,
∴ $\angle DBF = \angle BFC - \angle BDC = 20^{\circ}$,
∵ $BE$ 为角平分线,
∴ $\angle ABC = 2\angle DBF = 40^{\circ}$,
∴ $\angle BCF = 90^{\circ} - \angle ABC = 50^{\circ}$.
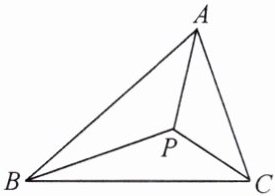
12. 如图,点 $ P $ 为 $ \triangle A B C $ 的内角平分线 $ B P $ 与 $ C P $ 的交点。求证:$ \angle B P C = 90 ^ { \circ } + \frac { 1 } { 2 } \angle B A C $。
证明:在 $\triangle ABC$ 中,$\angle ABC + \angle ACB + \angle BAC = 180^{\circ}$,∴ $\angle ABC + \angle ACB =$

证明:在 $\triangle ABC$ 中,$\angle ABC + \angle ACB + \angle BAC = 180^{\circ}$,∴ $\angle ABC + \angle ACB =$
$180^{\circ} - \angle BAC$
,∵ 点 $P$ 为 $\triangle ABC$ 的内角平分线 $BP$ 与 $CP$ 的交点,∴ $\angle PBC =$$\frac{1}{2}\angle ABC$
,$\angle PCB =$$\frac{1}{2}\angle ACB$
,∴ $\angle PBC + \angle PCB = \frac{1}{2}(\angle ABC + \angle ACB) = \frac{1}{2}($$180^{\circ} - \angle BAC$
$) =$$90^{\circ} - \frac{1}{2}\angle BAC$
,∴ $\angle BPC = 180^{\circ} - ($$90^{\circ} - \frac{1}{2}\angle BAC$
$) = 90^{\circ} + \frac{1}{2}\angle BAC$.
答案:
【解析】在 $\triangle ABC$ 中,$\angle ABC + \angle ACB + \angle BAC = 180^{\circ}$,
∴ $\angle ABC + \angle ACB = 180^{\circ} - \angle BAC$,
∵ 点 $P$ 为 $\triangle ABC$ 的内角平分线 $BP$ 与 $CP$ 的交点,
∴ $\angle PBC = \frac{1}{2}\angle ABC$,$\angle PCB = \frac{1}{2}\angle ACB$,
∴ $\angle PBC + \angle PCB = \frac{1}{2}(\angle ABC + \angle ACB) = \frac{1}{2}(180^{\circ} - \angle BAC) = 90^{\circ} - \frac{1}{2}\angle BAC$,
∴ $\angle BPC = 180^{\circ} - (90^{\circ} - \frac{1}{2}\angle BAC) = 90^{\circ} + \frac{1}{2}\angle BAC$.
∴ $\angle ABC + \angle ACB = 180^{\circ} - \angle BAC$,
∵ 点 $P$ 为 $\triangle ABC$ 的内角平分线 $BP$ 与 $CP$ 的交点,
∴ $\angle PBC = \frac{1}{2}\angle ABC$,$\angle PCB = \frac{1}{2}\angle ACB$,
∴ $\angle PBC + \angle PCB = \frac{1}{2}(\angle ABC + \angle ACB) = \frac{1}{2}(180^{\circ} - \angle BAC) = 90^{\circ} - \frac{1}{2}\angle BAC$,
∴ $\angle BPC = 180^{\circ} - (90^{\circ} - \frac{1}{2}\angle BAC) = 90^{\circ} + \frac{1}{2}\angle BAC$.
13. 定义:一个三角形的一边长是另一边长的 2 倍,这样的三角形叫作“倍长三角形”。若 $ \triangle A B C $ 是“倍长三角形”,有两条边的长分别为 2 和 3,求第三条边的长。
答案:
【解析】设三角形 $ABC$ 中,第三条边 $AB = x$,$AC = 2$,$BC = 3$,① 当 $AB = 2AC$,即 $x = 4$,
∴ $\triangle ABC$ 三边分别是 2,3,4,符合题意;② 当 $AB = 2BC$,即 $x = 6$,
∴ $\triangle ABC$ 三边分别是 2,3,6,
∵ $2 + 3 < 6$,
∴ 此时不能构成三角形,这种情况不存在;③ 当 $AC = 2AB = 2$,即 $x = 1$,
∴ $1 + 2 = 3$,
∴ 此时不能构成三角形,这种情况不存在;④ 当 $BC = 2AB = 3$,即 $x = 1.5$,
∴ $\triangle ABC$ 三边分别是 1.5,2,3,符合题意. 综上所述,第三条边的长为是 4 或 1.5.
∴ $\triangle ABC$ 三边分别是 2,3,4,符合题意;② 当 $AB = 2BC$,即 $x = 6$,
∴ $\triangle ABC$ 三边分别是 2,3,6,
∵ $2 + 3 < 6$,
∴ 此时不能构成三角形,这种情况不存在;③ 当 $AC = 2AB = 2$,即 $x = 1$,
∴ $1 + 2 = 3$,
∴ 此时不能构成三角形,这种情况不存在;④ 当 $BC = 2AB = 3$,即 $x = 1.5$,
∴ $\triangle ABC$ 三边分别是 1.5,2,3,符合题意. 综上所述,第三条边的长为是 4 或 1.5.
查看更多完整答案,请扫码查看


