《2025年暑期衔接培优集训七年级升八年级数学》

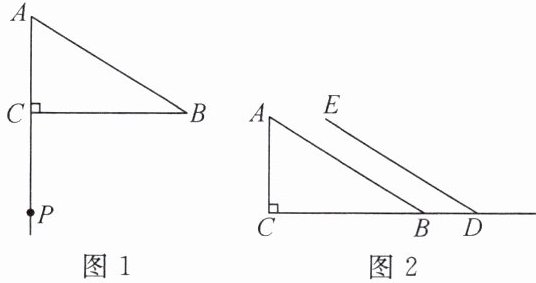
9. 如图,已知$Rt\triangle ACB$,$∠ACB= 90^{\circ}$,请结合下述要求完成作图并回答相应问题：
(1)如图$1$,平移图中的线段$AB$,使点$A移到点P$的位置,请使用不含刻度的直尺与圆规作出平移后的线段$PQ$(不写作法,保留作图痕迹)；
(2)如图$2$,将线段$AB水平向右平移m个单位得到线段ED$,请使用不含刻度的直尺与圆规作出点$C平移后的对应点F$(不写作法,保留作图痕迹),若点$F在点B$的左侧,$CD= 12$,$FB= 5.5$,则$m= $$\frac{13}{4}$.

答案：
【解析】
(1) 如图 1，分别以点P、B为圆心，线段AB、AP长度为半径作弧，两弧交于点Q，连接PQ，则直线PQ为所求；

(2) 如图 2，以点D为圆心，线段BC长度为半径作弧，交线段BC于点F，则点F为所求；$\frac{13}{4}$。

10. 如图,$OC平分∠AOB$,将射线$OB沿着OA$方向平移,得到射线$DF$,交$OC于点N$,点$F在点N$的右侧.
(1)若$∠AOB= 60^{\circ}$,求$∠CNF$的度数.30°
(2)点$M是射线OA$上一点(不与点$D$,点$O$重合). 连接$MN$.
①若点$M在射线DA$上,延长$MN交OB于点E$,且$∠MEB-2∠CNF= 90^{\circ}$,求证：$NM\perp OA$.
②试判断$∠AOB+∠OMN与∠DNM$的数量关系,并说明理由.$∠AOB + ∠OMN = 180^{\circ} - ∠DNM$或$∠AOB + ∠OMN = 180^{\circ} + ∠DNM$

答案：
【解析】
(1) $\because OC$ 平分 $\angle AOB$，$\angle AOB = 60^{\circ}$，
$\therefore \angle AOC = \angle BOC = \frac{1}{2}\angle AOB = 30^{\circ}$，
由平移得，$OB // DF$，
$\therefore \angle CNF = \angle BOC = 30^{\circ}$；
(2) ① 证明：$\because OC$ 平分 $\angle AOB$，
$\therefore \angle AOC = \angle BOC = \frac{1}{2}\angle AOB$，
由平移得，$OB // DF$，
$\therefore \angle CNF = \angle BOC$，
$\therefore \angle AOB = 2\angle CNF$，
$\because \angle MEB = 180^{\circ} - \angle MEO = \angle EMO + \angle EOM$，
$\angle MEB - 2\angle CNF = 90^{\circ}$，
$\therefore \angle EMO = 90^{\circ}$，
$\therefore NM \perp OA$；
② 点 $M$ 在射线 $DA$ 上时，
由平移得 $OB // DF$，
$\therefore \angle DNM = \angle OEM$，
$\because \angle AOB + \angle OMN + \angle OEM = 180^{\circ}$，
$\therefore \angle AOB + \angle OMN = 180^{\circ} - \angle DNM$，

点 $M$ 在线段 $OD$ 上时，
由平移得 $OB // DF$，
$\therefore \angle BOC = \angle FNC$，
$\because \angle MNC = 180^{\circ} - \angle MNO = \angle AOC + \angle OMN$，
$\angle MNC = \angle DNM + \angle CND$，
$\therefore \angle AOB + \angle OMN$
$= \angle AOC + \angle BOC + \angle OMN$
$= \angle MNC + \angle FNC$
$= \angle DNC + \angle FNC + \angle DNM$
$= 180^{\circ} + \angle DNM$。

综上所述，$\angle AOB + \angle OMN = 180^{\circ} - \angle DNM$ 或 $\angle AOB + \angle OMN = 180^{\circ} + \angle DNM$。