1. 问题引入:
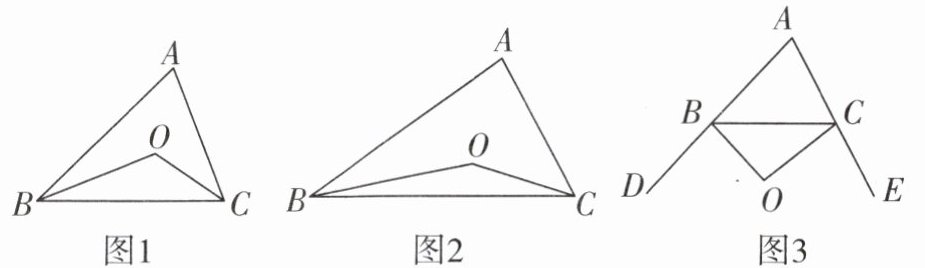
(1) 如图1所示,$\triangle ABC$中,点$O是\angle ABC和\angle ACB$的平分线的交点,若$\angle A= \alpha$,则$\angle BOC= $______(用$\alpha$表示),填空并说明理由;
如图2所示,$\angle OBC= \frac{1}{3}\angle ABC$,$\angle OCB= \frac{1}{3}\angle ACB$,若$\angle A= \alpha$,则$\angle BOC= $______(用$\alpha$表示),填空并说明理由.
(2) 如图3所示,$\angle OBC= \frac{1}{3}\angle DBC$,$\angle OCB= \frac{1}{3}\angle ECB$,若$\angle A= \alpha$,求$\angle BOC$的度数(用$\alpha$表示).

(1) 如图1所示,$\triangle ABC$中,点$O是\angle ABC和\angle ACB$的平分线的交点,若$\angle A= \alpha$,则$\angle BOC= $______(用$\alpha$表示),填空并说明理由;
如图2所示,$\angle OBC= \frac{1}{3}\angle ABC$,$\angle OCB= \frac{1}{3}\angle ACB$,若$\angle A= \alpha$,则$\angle BOC= $______(用$\alpha$表示),填空并说明理由.
(2) 如图3所示,$\angle OBC= \frac{1}{3}\angle DBC$,$\angle OCB= \frac{1}{3}\angle ECB$,若$\angle A= \alpha$,求$\angle BOC$的度数(用$\alpha$表示).
答案:
$(1)$ $90^{\circ}+\frac{1}{2}\alpha$;$120^{\circ}+\frac{1}{3}\alpha$
$(2)$ $\angle BOC = 120^{\circ}-\frac{1}{3}\alpha$
$(2)$ $\angle BOC = 120^{\circ}-\frac{1}{3}\alpha$
查看更多完整答案,请扫码查看


