《2025年高中新课程学习指导数学选择性必修第三册人教版》

[典例3] 关于两个变量x和y的7组数据如下表所示.

计算两个变量的样本相关关系，并据此判断x与y之间是否具有线性相关关系.

答案： 解：
∵$\overline{x}=\frac{1}{7}\times(21 + 23 + 25 + 27 + 29 + 32 + 35)\approx27.4$，$\overline{y}=\frac{1}{7}\times(7 + 11 + 21 + 24 + 66 + 115 + 325)\approx81.3$，$\sum_{i = 1}^{7}x_{i}^{2}=21^{2}+23^{2}+25^{2}+27^{2}+29^{2}+32^{2}+35^{2}=5414$，$\sum_{i = 1}^{7}x_{i}y_{i}=21\times7 + 23\times11 + 25\times21 + 27\times24 + 29\times66 + 32\times115 + 35\times325 = 18542$，$\sum_{i = 1}^{7}y_{i}^{2}=7^{2}+11^{2}+21^{2}+24^{2}+66^{2}+115^{2}+325^{2}=124393$，$\therefore r=\frac{\sum_{i = 1}^{7}x_{i}y_{i}-7\overline{x}\overline{y}}{\sqrt{\sum_{i = 1}^{7}x_{i}^{2}-7\overline{x}^{2}}\cdot\sqrt{\sum_{i = 1}^{7}y_{i}^{2}-7\overline{y}^{2}}}$ $=\frac{18542 - 7\times27.4\times81.3}{\sqrt{5414 - 7\times27.4^{2}}\cdot\sqrt{124393 - 7\times81.3^{2}}}\approx0.8375$
∵r≈0.8375与1比较接近，
∴x与y具有线性相关关系.

减脂是现在很热门的话题，人体内的脂肪会受年龄的影响而不同，为了解脂肪和年龄是否有关系，某兴趣小组得到年龄和脂肪观测值的如下数据：

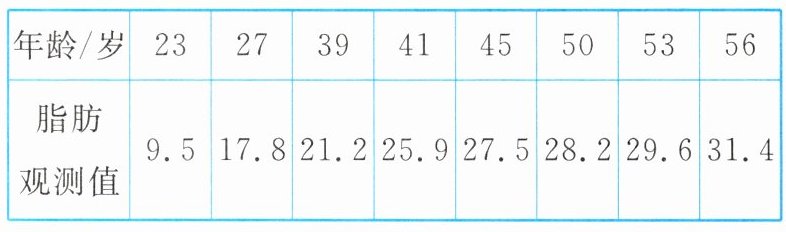
并计算得$\overline{x}\approx41.8,\overline{y}\approx23.9,\sum_{i = 1}^{8}x_{i}^{2}=14930,\sum_{i = 1}^{8}y_{i}^{2}\approx4941,\sum_{i = 1}^{8}x_{i}y_{i}=8562.5$.求年龄和脂肪观测值的样本相关系数（结果精确到0.01）.

答案： 解：$r=\frac{\sum_{i = 1}^{8}x_{i}y_{i}-8\overline{x}\overline{y}}{\sqrt{(\sum_{i = 1}^{8}x_{i}^{2}-8\overline{x}^{2})(\sum_{i = 1}^{8}y_{i}^{2}-8\overline{y}^{2})}}$ $\approx\frac{8562.5 - 8\times41.8\times23.9}{\sqrt{(14930 - 8\times41.8^{2})(4941 - 8\times23.9^{2})}}$ $=\frac{570.34}{\sqrt{952.08\times371.32}}\approx\frac{570.34}{594.58}\approx0.96$

[典例4] 某校高三（1）班的学生每周用于数学学习的时间x（单位：h）与数学平均成绩y（单位：分）之间的数据如表格所示.

（1）画出散点图；
（2）请判断数学学习的时间与数学平均成绩之间的相关关系的类型、相关程度和变化趋势的特征.

答案：
解：
(1)根据表中数据画出散点图，如图. 从散点图看，数学成绩与学习时间线性相关.
(2)由已知数据求得$\overline{x}=17.4$，$\overline{y}=74.9$，$\sum_{i = 1}^{10}x_{i}^{2}=3182$，$\sum_{i = 1}^{10}y_{i}^{2}=58375$，$\sum_{i = 1}^{10}x_{i}y_{i}=13578$，所以样本相关系数 $r=\frac{\sum_{i = 1}^{10}x_{i}y_{i}-10\overline{x}\overline{y}}{\sqrt{(\sum_{i = 1}^{10}x_{i}^{2}-10\overline{x}^{2})(\sum_{i = 1}^{10}y_{i}^{2}-10\overline{y}^{2})}}\approx0.920$由样本相关系数知，数学学习时间与数学平均成绩呈正线性相关，因为r≈0.920与1接近，所以数学学习时间与数学成绩相关程度很高，且随着学习时间的增加，相应的学习成绩升高.