《2025年高中新课程学习指导数学选择性必修第三册人教版》

2. 某校高三共有三个班，其各班人数如下表:

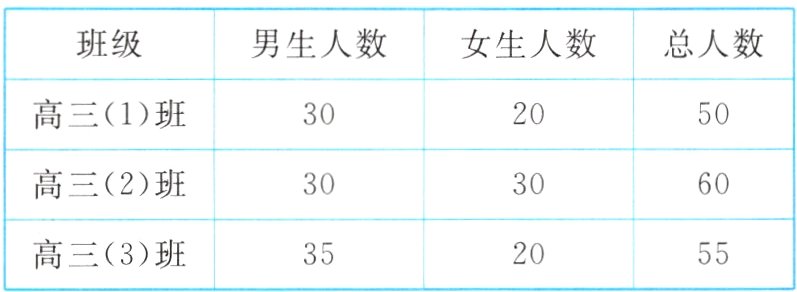
（1）从三个班中选一名学生担任学生会主席，有多少种不同的选法？
（2）从高三（1）班、高三（2）班男生中或从高三（3）班女生中选一名学生担任学生会生活部长，有多少种不同的选法？

答案： 2.解：
(1)从三个班中任选一名学生，可分三类：
第1类，从高三
(1)班任选一名学生，有50种不同选法；
第2类，从高三
(2)班任选一名学生，有60种不同选法；
第3类，从高三
(3)班任选一名学生，有55种不同选法.
由分类加法计数原理知，不同的选法种数为
$N = 50 + 60 + 55 = 165$.
(2)由题设知共有三类方案：
第1类，从高三
(1)班男生中任选一名学生，有30种不同选法；
第2类，从高三
(2)班男生中任选一名学生，有30种不同选法；
第3类，从高三
(3)班女生中任选一名学生，有20种不同选法.
由分类加法计数原理知，不同的选法种数为
$N = 30 + 30 + 20 = 80$.

[典例2] 有6名同学报名参加三个智力竞赛项目，在下列情况下各有多少种不同的报名方法？（不一定6名同学都参加）
（1）每人恰好参加一项，每项人数不限；
（2）每项限报一人，且每人至多参加一项.
[尝试解题]

答案： 解：
(1)每人都可以从这三个智力竞赛项目中选报一项，各有3种不同的报名方法.
根据分步乘法计数原理，可得不同的报名方法种数为$3^6 = 729$.
(2)因为每项限报一人，且每人至多参加一项，所以可由项目选人.第一个项目有6种选法，第二个项目有5种选法，第三个项目有4种选法.根据分步乘法计数原理，可得不同的报名方法种数为6×5×4 = 120.

1. 为响应“节约粮食”的号召，某同学决定在某食堂提供的2种主食、3种素菜、2种大荤、4种小荤中选取1种主食、1种素菜、1种荤菜作为今日伙食，并在用餐时积极践行“光盘行动”，则不同的选取方法有（ ）
A. 48种
B. 36种
C. 24种
D. 12种

答案： 1.B

2. 若本例条件变为若每项限报一人，但每人参加的项目不限，有多少种不同的报名方法？

答案： 2.解：因为每人参加的项目不限，所以每一个项目都可以从这6人中选出1人参加.根据分步乘法计数原理，可得不同的报名方法种数为$6^3 = 216$.