《2025年情境题提思维六年级数学下册北师大版》

1. 莫比乌斯带是将一张纸条扭转( )后，再将两端粘起来做成的纸环，与普通纸环不同的是，该纸环只有 1 个面，1 条边。图中莫比乌斯带上的蚂蚁( )(填“需要”或“不需要”)爬过纸带边缘就能吃到纸带上任意一点的面包。

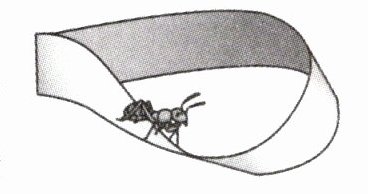
答案： 180°@@不需要

2. 下列造型应用了莫比乌斯带原理的是( )。


A. ①②③
B. ①②④
C. ①③④
D. ②③④

答案： A

3. 如图，取一张长为 40 cm、宽为 5 cm 的纸条，在纸条的两个面中间都画一条线，将其扭转 180°，然后再把两端连接、用胶粘起来，蚂蚁从 A 点出发，沿着所画的线爬行。蚂蚁能爬回 A 点吗？如果能，蚂蚁至少爬行多少厘米？( 接口处忽略不计)

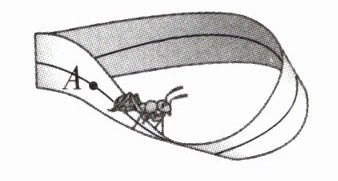
答案： 蚂蚁能爬回A点 需要爬行的最短距离为纸条长度的2倍，即40×2 = 80(cm) 答：蚂蚁能爬回A点，蚂蚁爬回A点至少爬行80厘米。

4. 奇奇用一张长 18 cm、宽 5 cm 的长方形纸条做了一个纸环，如图①，妙妙用同样的纸条做了一个莫比乌斯带，如图②，他们都从纸环连接处 A 点开始，沿着一个方向涂色，直到再次回到连接处为止，分别求两人涂色区域的面积。( 接口处忽略不计)

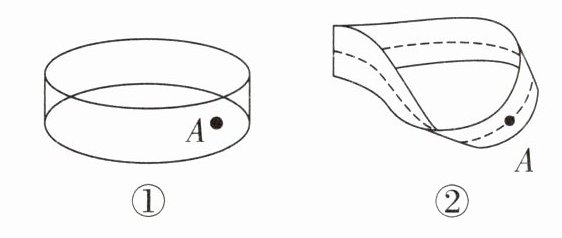
答案： 18×5 = 90(cm²) 18×5×2 = 180(cm²) 答：奇奇的涂色面积为90 cm²，妙妙的涂色面积是180 cm²。

5. 奇奇在一张纸条的中间画一条虚线，做成莫比乌斯带后再沿虚线剪开，会得到怎样的结果？如果沿三等分线剪开呢？

答案： 答：沿二等分线剪开，莫比乌斯带变成了一个窄一点的大纸环，此时这个纸环不是莫比乌斯带。 沿三等分线剪开，剪开后是两个套在一起的纸环，其中一个是窄一点的大纸环(不是莫比乌斯带)，另一个是窄一点的小纸环(仍是莫比乌斯带，是原来分成三份中的中间部分形成的)。

6. 通过课堂学习我们已经知道，将一张纸条扭转 180°再将两端粘起来即可得到一个神奇的莫比乌斯带，那么如果扭转 360°还是莫比乌斯带吗？如果扭转 540°呢？

答案：