《2025年情境题提思维六年级数学下册北师大版》

9.（P10第7题变式）奇奇受“乌鸦喝水”的故事启发，他先将400 mL的水倒入圆柱体容器中（如图所示），此时量得水深是5 cm，在放入体积相同的玻璃小球后，溢出了20 mL水，那么每个玻璃小球的体积是多少立方厘米？

答案： 圆柱的底面积：$400÷5 = 80(cm^2)$ $20mL = 20cm^3$ 小球的总体积：$80×(17 - 5)+20 = 980(cm^3)$ $980÷7 = 140(cm^3)$ 答：每个玻璃小球的体积是140立方厘米。

10.（教参P6样题13变式）妙妙有4个大小相同的圆柱形橡皮泥，她将4个橡皮泥叠起来形成了一个大圆柱体，表面积减少了75.36 cm²；如果沿着一个圆柱形橡皮泥的底面直径将其截成两个半圆柱体，则它的表面积增加80 cm²，原来每个圆柱形橡皮泥的表面积和体积分别是多少？

答案： 直径：$75.36÷6÷3.14 = 4(cm)$ 半径：$4÷2 = 2(cm)$ 高：$80÷2÷4 = 10(cm)$ 表面积：$3.14×2^2×2 + 2×3.14×2×10 = 150.72(cm^2)$ 体积：$3.14×2^2×10 = 125.6(cm^3)$ 答：原来每个圆柱形橡皮泥的表面积是150.72平方厘米，体积是125.6立方厘米。

11. 如图，A和B都是高度为10 cm的圆柱形容器，底面半径分别为1 cm和2 cm。一水龙头单独向A注水，用1分可以注满。现在两个容器在它们高度一半处用一个细管连通（连通管子的厚度、容积忽略不计），仍用该龙头向A注水。求4分时，A容器中水的高度是多少厘米？

答案： $3.14×1^2×10 = 31.4(cm^3)$ $31.4×4 = 125.6(cm^3)$ $3.14×(1^2 + 2^2)=15.7(cm^2)$ $125.6÷15.7 = 8(cm)$ 8 cm大于细管的高度，小于容器的高度，说明4分时水面已超过细管且未注满。 答：4分时，A容器中水的高度是8厘米。 点拨：由题意可知向A容器单独注水，1分可以注满，所以可以求出1分注水体积，且B容器的底面半径是A容器底面半径的2倍，所以B容器的容积就是A容器的4倍，那么两个容器都注满就需要1 + 4 = 5(分)，也就是说5÷2 = 2.5(分)时两个容器都可以注入5 cm高的水，2.5分以后的时间两个容器的水位同时上升相同高度，所以用4分注水量除以A、B两个容器底面积的和就是它们的水面高度。

12. 一名工人要将如图所示的长方体木块削成一个圆锥，怎样削才能使削成的圆锥体积最大，计算并说明理由。

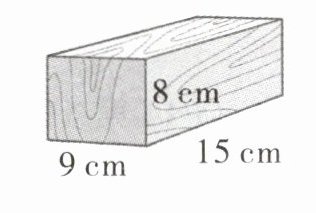
答案： 以长为9 cm，宽为8 cm的长方形的面作为圆锥底面削，才能使削成的圆锥体积最大。 理由如下： ①当以长为15 cm，宽为9 cm的长方形的面作为圆锥底面时，底面直径为9 cm，高为8 cm 所削成的圆锥体积：$\frac{1}{3}×3.14×(9÷2)^2×8 = 169.56(cm^3)$ ②当以长为15 cm，宽为8 cm的长方形的面作为圆锥底面时，底面直径是8 cm，高为9 cm 所削成的圆锥体积：$\frac{1}{3}×3.14×(8÷2)^2×9 = 150.72(cm^3)$ ③当以长为9 cm，宽为8 cm的长方形的面作为圆锥底面时，底面直径是8 cm，高为15 cm 所削成的圆锥体积：$\frac{1}{3}×3.14×(8÷2)^2×15 = 251.2(cm^3)$ $251.2 cm^3＞169.56 cm^3＞150.72 cm^3$ 所以以长为9厘米，宽为8厘米的长方形的面作为圆锥底面削，才能使削成的圆锥体积最大。 点拨：长方体有长、宽、高三种棱长，因此需要分三种情况进行计算：①以长和宽的面为底，高为圆锥的高；②以长和高的面为底，宽为圆锥的高；③以宽和高的面为底，长为圆锥的高，将三种体积的大小进行比较即可。