第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
例 1 按照 1 : 2 的比画出下图三角形 $ABC$ 缩小后的三角形 $A'B'C'$。
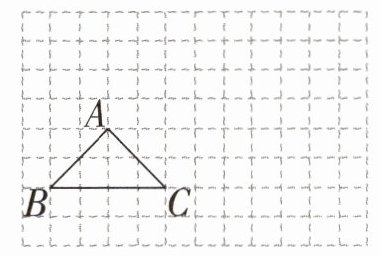
操作步骤:(1)原来三角形的 $BC$ 边长为( )格,按照 1 : 2 的比缩小后,应为( )格;同理缩小后的三角形各边长 : 原三角形的各边长 =( ) : ( );
(2)在网格中的某个格点上选取一个点,从这个点开始,这个点为图形的某个顶点,依次描出其他的点,其中线段长缩小为原来的 $\frac{1}{2}$,各角度保持不变,然后把各点顺次连接。在上图中画出缩小后的图形。
例 2 如图为三角形 $ABC$,以点 $O$ 为位似中心,画缩小后的三角形 $A'B'C'$,使得它与三角形 $ABC$ 位似,且位似比为 1 : 2。|
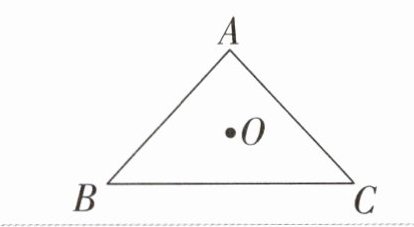
操作步骤:(1)在三角形 $ABC$ 中定点 $O$ 在初中叫作位似中心;
(2)以点 $O$ 为端点作射线 $OA,OB,OC$;
(3)分别在射线 $OA,OB,OC$ 上取点 $A',B',C'$使得 $\frac{OA'}{OA}=\frac{OB'}{OB}=\frac{OC'}{OC}=( )$,这个比就叫作位似比;
(4)连接 $A'B',B'C',C'A'$,所得三角形 $A'B'C'$ 即为所求。在上图中画出缩小后的图形。
思考
(1)分别补全上面两道题的操作步骤及答案。
(2)观察例 1 和例 2,我发现:①相同点:小学的图形缩放与初中的图形位似两者都( )(填“改变”或“不改变”)图形大小,( )(填“改变”或“不改变”)图形形状。
②不同点:初中变化后的图形与原图形对应点的连线都( )(填“经过同一点”或“不经过同一点”),这个点称为( );小学新图形与原图形各个对应边( )(填“满足”或“不满足”)一定的比例关系。
除此之外,你还能发现什么呢?

操作步骤:(1)原来三角形的 $BC$ 边长为( )格,按照 1 : 2 的比缩小后,应为( )格;同理缩小后的三角形各边长 : 原三角形的各边长 =( ) : ( );
(2)在网格中的某个格点上选取一个点,从这个点开始,这个点为图形的某个顶点,依次描出其他的点,其中线段长缩小为原来的 $\frac{1}{2}$,各角度保持不变,然后把各点顺次连接。在上图中画出缩小后的图形。
例 2 如图为三角形 $ABC$,以点 $O$ 为位似中心,画缩小后的三角形 $A'B'C'$,使得它与三角形 $ABC$ 位似,且位似比为 1 : 2。|

操作步骤:(1)在三角形 $ABC$ 中定点 $O$ 在初中叫作位似中心;
(2)以点 $O$ 为端点作射线 $OA,OB,OC$;
(3)分别在射线 $OA,OB,OC$ 上取点 $A',B',C'$使得 $\frac{OA'}{OA}=\frac{OB'}{OB}=\frac{OC'}{OC}=( )$,这个比就叫作位似比;
(4)连接 $A'B',B'C',C'A'$,所得三角形 $A'B'C'$ 即为所求。在上图中画出缩小后的图形。
思考
(1)分别补全上面两道题的操作步骤及答案。
(2)观察例 1 和例 2,我发现:①相同点:小学的图形缩放与初中的图形位似两者都( )(填“改变”或“不改变”)图形大小,( )(填“改变”或“不改变”)图形形状。
②不同点:初中变化后的图形与原图形对应点的连线都( )(填“经过同一点”或“不经过同一点”),这个点称为( );小学新图形与原图形各个对应边( )(填“满足”或“不满足”)一定的比例关系。
除此之外,你还能发现什么呢?
答案:
4
@@2
@@1
@@2
@@画图如下。
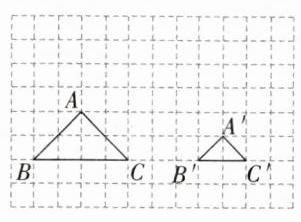
@@$\frac{1}{2}$
@@画图如下。
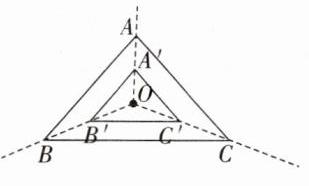
@@改变
@@不改变
@@经过同一点
@@位似中心
@@满足
@@我发现:小学变化后的新图形与原图形对应点的连线也经过同一点;初中变化后的新图形与原图形的对应边也成比例。(答案不唯一)
4
@@2
@@1
@@2
@@画图如下。

@@$\frac{1}{2}$
@@画图如下。

@@改变
@@不改变
@@经过同一点
@@位似中心
@@满足
@@我发现:小学变化后的新图形与原图形对应点的连线也经过同一点;初中变化后的新图形与原图形的对应边也成比例。(答案不唯一)
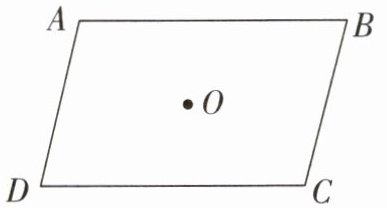
右图为平行四边形 $ABCD$,以点 $O$ 为位似中心画缩小后的平行四边形 $A'B'C'D'$,使得它与平行四边形 $ABCD$ 位似,且位似比为 $\frac{1}{2}$。

答案:
画图如下。
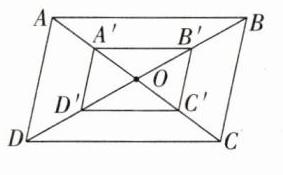
画图如下。

查看更多完整答案,请扫码查看


