《2025年情境题提思维六年级数学下册北师大版》

1. 连线课堂·图形的相关计算 在圆柱的展开图上标出对应的数据,并填空。(结果保留π)

圆柱的表面积 = 侧面积+(底面积)×2,
侧面积=(底面圆周长)×6 cm =( ),圆柱的底面积 =( ),
圆柱的表面积=( )+( )×2=( )。

答案：

底面积@@$4\pi cm$@@$24\pi cm^{2}$@@$4\pi cm^{2}$@@$24\pi cm^{2}$@@$4\pi cm^{2}$@@$32\pi cm^{2}$

2. (P5问题2变式)圆柱的侧面展开图不可能是( )。
A. 正方形
B. 长方形
C. 平行四边形
D. 梯形

答案： D

3. (教参P6样题5变式)如果一个圆柱的侧面积是125.6 cm²,高是10 cm,那么它的底面半径是( )cm。
A. 2
B. 4
C. 6
D. 8

答案： A

4. (P5问题4变式)如图,太阳能热水器顶部是一个密封的圆柱形水桶,制作一个这样的水桶至少需要( )cm²的不锈钢材料。

答案： 12490. 92

5. (P6第2题变式)计算下列圆柱的表面积。

答案： $2×2×3.14×7 + 2×3.14×2^{2}=113.04(cm^{2})$@@$2×3.14×(9.42÷3.14÷2)^{2}+9.42×5 = 61.23(cm^{2})$

6. (P6第1题变式)如图,将一个圆柱的侧面展开,宽增加4 cm,长不变,此时围成的圆柱的表面积增加75.36 cm²,这个圆柱的底面积是多少平方厘米?

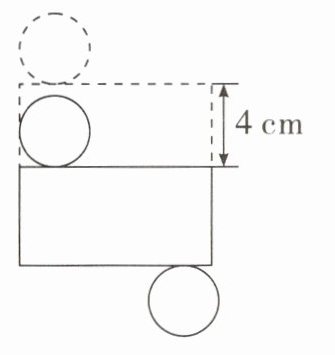
答案： 表面积增加的部分就是高为4 cm的圆柱形的侧面积 底面半径：$75.36÷4÷2÷3.14 = 3(cm)$ 底面积：$3.14×3^{2}=28.26(cm^{2})$ 答：这个圆柱的底面积是28.26平方厘米。

7. 如图是一张长方形纸板,按图示剪下阴影部分刚好可以做一个圆柱(接头处用的纸板忽略不计),做成的圆柱的表面积是多少平方厘米?

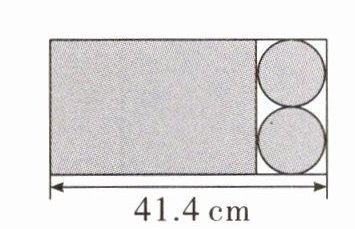
答案： 圆柱的底面直径：$41.4÷(1 + 3.14)=10(cm)$ 圆柱的高：$2×10 = 20(cm)$ 圆柱的表面积：$3.14×10×20+3.14×(10÷2)^{2}×2 = 785(cm^{2})$ 答：做成的圆柱的表面积是785平方厘米。 点拨 在剪下的阴影部分中，长方形的长 + 1个圆的直径 = 做成的圆柱底面周长 + 2个半径。