《2025年情境题提思维六年级数学下册北师大版》

8.（P11问题2变式）谷物在堆积时大多会形成圆锥形状，某农场运回的小麦在空地上形成了一个底面直径为14 m，高为6 m的麦堆，现要用容积为8 m³的粮食桶进行储存，至少需要多少个这样的粮食桶才能把小麦全部装完?

答案： 麦堆的体积：$\frac{1}{3}×3.14×(14÷2)^2×6 = 307.72(m^3)$ $307.72÷8 = 38.465≈39$(个) 答：至少需要 39 个这样的粮食桶才能把小麦全部装完。

9.（P12第5题变式）农场的墙角堆放了小麦，如图，麦堆顶点在两墙交界处（两面墙垂直），它的形状可以看作圆锥的一部分，已知麦堆不靠墙部分的底面周长是3.14 m，麦堆高3 m，若每立方米小麦重720 kg，那么墙角这堆小麦重多少千克?

答案： 麦堆的半径：$3.14×4÷3.14÷2 = 2(m)$ 麦堆的体积：$\frac{1}{4}×\frac{1}{3}×3.14×2^2×3 = 3.14(m^3)$ $3.14×720 = 2260.8(kg)$ 答：墙角这堆小麦重 2260.8 千克。

10.（教参P6样题13变式）有两个完全相同的小木块，将它们拼在一起后形成了一个圆锥体（如图所示），已知圆锥体的高为10 cm，拼成后的表面积比原来减少了120 cm²，现在这个圆锥体木块的体积是多少立方厘米?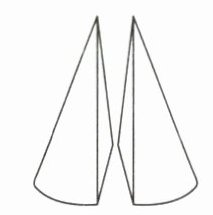

答案： $120÷2÷10÷\frac{1}{2} = 12(cm)$ 体积：$\frac{1}{3}×3.14×(12÷2)^2×10 = 376.8(cm^3)$ 答：现在这个圆锥体木块的体积是 376.8 立方厘米。

11. 把如图所示的一块直角三角形木板绕斜边所在直线旋转一周，得到的立体图形的体积是( )dm³。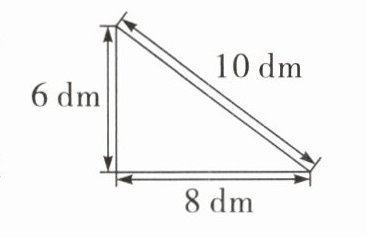

答案： 241.152

12. 如图是一个顶部为近似圆锥形的高脚杯。杯中放着一块柠檬，柠檬的体积为$\frac{112}{3}\pi$ cm³，在杯中倒满水后，再把柠檬拿出来，此时水面半径是2 cm，求此时杯中水面高度到桌面的距离。

答案： 杯子的容积：$\frac{1}{3}×\pi×(8÷2)^2×8 = \frac{128}{3}\pi(cm^3)$ 水的体积：$\frac{128}{3}\pi - \frac{112}{3}\pi = \frac{16}{3}\pi(cm^3)$ $\frac{16}{3}\pi÷\frac{1}{3}÷\pi÷2^2 = 4(cm)$ $4 + 5 = 9(cm)$ 答：此时杯中水面高度到桌面的距离是 9 厘米。 点拨 杯子的容积减去柠檬的体积是水的体积，再结合已知的水面半径，即可求解此时杯中的水面高度。