《2026年全品中考复习方案九年级物理全一册人教版》

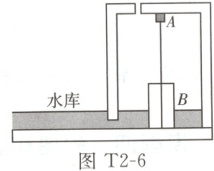
3. (2023 泸州)科创小组设计了水库自动泄洪控制装置,将其制成顶部开有小孔的模型,如图 T2-6 所示。其中$A$为压力传感器,$B$是密度小于水且不吸水的圆柱体,能沿固定的光滑细杆在竖直方向自由移动。当模型内水深$h_0 = 15\ cm$时,$B$与模型底面刚好接触且压力为零。水面上涨到设计的警戒水位时,圆柱体对压力传感器的压力为$2\ N$,触发报警装置,开启泄洪阀门。已知圆柱体$B$的底面积$S_B = 50\ cm^2$、高$h_B = 25\ cm$,$g$取$10\ N/kg$。
(1)★★当$B$对模型底面压力$F_1 = 2.5\ N$时,求模型内水深$h_1$。

(2)★★刚触发报警装置时,求$B$浸入水中的深度$h_2$。
(3)★★★为了提高防洪安全性,警戒水位需要比原设计低$5\ \text{cm$,在$B$的上方加上与$B$同材质同底面积的圆柱体$C$,求圆柱体$C$的高度$h_3$。
思路点拨
利用临界条件求出$B$所受的重力$G$,然后根据已知条件求$B$对模型底面的压力为$2.5\ N$时所受浮力$F_{ 浮}$,再由$F_{ 浮} \to V_{ 排} \to h_1$。
(2)刚触发报警装置时,求$B$浸入水中的深度和$B$的高度求出$A$到水面的距离,根据警戒水位需要比原设计低$5\ cm$再求出此时$A$到水面的距离,进而表示出$BC$整体排开水的深度,根据体积公式和阿基米德原理表示出$BC$整体受到的浮力,根据体积公式、密度公式和$G = mg$表示出$BC$整体的重力,根据力的平衡条件表示出$BC$整体受到的浮力、圆柱体对压力传感器的压力和$BC$整体所受重力之间的关系,解方程求出圆柱体$C$的高度。

答案： 3.解:
(1)当模型内水深h₀=15cm时，B排开水的体积:V₀=S₁h₀=50cm²×15cm=750cm³,由B与模型底面刚好接触且压力为零可知，此时B恰好处于漂浮状态，
由物体的漂浮条件可知,B所受的重力:GB=F浮=ρ水gV₀=1.0×10³kg/m³×10N/kg×750×10⁻⁶m³=7.5N,
由力的平衡条件可知，当B对模型底面压力F₁=2.5N时，B受到的浮力:F浮'=GB−F₁=7.5N−2.5N=5N,
由F浮=ρ液gV排可知,此时B排开水的体积:V₁=$\frac{F_{浮}'}{\rho_{水}g}$=$\frac{5N}{1.0×10^{3}kg/m^{3}×10N/kg}$=5×10⁻⁴m³=500cm³,
由V=Sh可知，此时B浸入水中的深度即模型内水的深度:h₁=$\frac{V_{1}}{S_{B}}$=$\frac{500cm^{3}}{50cm^{2}}$=10cm。
(2)刚触发报警装置时圆柱体对压力传感器的压力F₂=2N，由力的平衡条件可知，此时B受到的浮力:F浮"=GB+F₂=7.5N+2N=9.5N,
由F浮=ρ液gV排可知,B排开水的体积:V₂=$\frac{F_{浮}''}{\rho_{水}g}$=$\frac{9.5N}{1.0×10^{3}kg/m^{3}×10N/kg}$=9.5×10⁻⁴m³=950cm³,
由V=Sh可知,此时B浸入水中的深度:h₂=$\frac{V_{2}}{S_{B}}$=$\frac{950cm^{3}}{50cm^{2}}$=19cm。
(3)由刚触发报警装置时B浸入水中的深度和B的高度可知，A到水面的距离:hA=hB−h₂=25cm−19cm=6cm,
警戒水位需要比原设计低5cm，则触发报警装置时，A到水面的距离应为hA'=hA+5cm=6cm+5cm=11cm,
则BC整体排开水的深度:hBC=h₃+hB−hA'=h₃+25cm−11cm=h₃+14cm,
BC整体排开水的体积:VBC=S₁hBC=50cm²×(h₃+14cm)=50×10⁻⁴m²×(0.01h₃+0.14m),
此时BC整体受到的浮力:F浮"'=ρ水gVBC=1.0×10³kg/m³×10N/kg×(50×10⁻⁴m²×0.01h₃+7×10⁻⁴m³),
BC整体的体积:V=S₁(h₃+hB)=50cm²×(h₃+25cm)=50×10⁻⁴m²×(0.01h₃+1.25×10⁻³m³),
由G=mg可知,B的质量:mB=$\frac{G_{B}}{g}$=$\frac{7.5N}{10N/kg}$=0.75kg=750g,
B的体积:VB=S₁hB=50cm²×25cm=1250cm³,
则B的密度:ρB=$\frac{m_{B}}{V_{B}}$=$\frac{750g}{1250cm^{3}}$=0.6g/cm³=0.6×10³kg/m³,
C与B是同样材质,则BC整体所受的重力:G=mg=ρBgV=0.6×10³kg/m³×10N/kg×(50×10⁻⁴m²×0.01h₃+1.25×10⁻³m³),
由力的平衡条件可知,F浮"'=G+F₂,
即1.0×10³kg/m³×10N/kg×(50×10⁻⁴m²×0.01h₃+7×10⁻⁴m³)=0.6×10³kg/m³×10N/kg×(50×10⁻⁴m²×0.01h₃+1.25×10⁻³m³)+2N,解得h₃=12.5cm。