《2026年全品中考复习方案九年级物理全一册人教版》

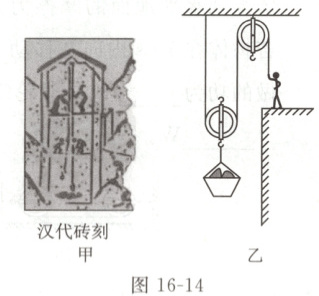
例 10（2025 遂宁）我国很早就有使用滑轮的记载，如图 16-14 甲所示的汉代砖刻便记录了矿山使用滑轮做起吊机械的场景。借助如图乙所示的装置（篮子质量不计），质量为$60 kg$的采矿工人用$400 N$的拉力将$70 kg$的矿石从矿坑匀速提起，$10 s$内矿石上升了$2 m$。求：（忽略绳重及滑轮的摩擦，$g$取$10 N/kg$）

（1）绳子自由端移动的速度。
（2）此滑轮组的机械效率。
（3）若工作时矿工双脚与地面的接触面积为$400 cm^2$，他对水平地面的压强大小。

答案： 例 10 解：（1）由图乙可知，$n = 2$，
绳子自由端移动的距离：
$s = nh = 2×2m = 4m$，
绳子自由端移动的速度：$v=\frac{s}{t}=\frac{4m}{10s}=0.4m/s$。
(2)矿石的重力：
$G = mg = 70kg×10N/kg = 700N$，
此滑轮组的机械效率：$\eta=\frac{W_{有用}}{W_{总}}=\frac{Gh}{Fs}=\frac{Gh}{Fnh}=\frac{G}{nF}=\frac{700N}{2×400N}=0.875 = 87.5\%$。
(3)工人的重力：$G_{人}=m_{人}g = 60kg×10N/kg = 600N$，
工作时矿工对水平地面的压力等于他的重力与绳子拉力之差，即：
$F_{压}=G_{人}-F = 600N - 400N = 200N$，
他对水平地面的压强：$p=\frac{F_{压}}{S}=\frac{200N}{400×10^{-4}m^{2}} = 5000Pa$。

例 11 滑轮图像题（2025 扬州仪征一模）如图 16-15 甲所示是一种新型吊运设备的简化模型示意图，定滑轮的轴和电动机均固定在 B 点。在一次作业中，该吊运设备匀速竖直提升物体，此时滑轮组的机械效率为$80\%$，被提升的物体上升的速度为$0.5 m/s$，电动机做的功跟时间的变化关系如图乙所示。不考虑滑轮组绳子的质量、滑轮与轴和绳子间的摩擦。求：
（1）此次作业中电动机的功率。
（2）此次作业中被提升的物体受到的重力。
（3）动滑轮的总重力。

答案： 例 11 解：
(1) 由图乙知，当$t = 1$ s 时，电动机做的总功$W_{总}=300$ J，
则电动机的功率：$P_{总}=\frac{W_{总}}{t}=\frac{300\ J}{1\ s} = 300$ W。
(2) 由$\eta=\frac{W_{有用}}{W_{总}}=\frac{P_{有用}t}{P_{总}t}=\frac{P_{有用}}{P_{总}}$可得，有用功功率：$P_{有用}=\eta P_{总}=80\%×300\ W=240$ W，
由$P_{有用}=\frac{W_{有用}}{t}=\frac{Gh}{t}=Gv_{物}$可得，被提升物体的重力：$G=\frac{P_{有用}}{v}=\frac{240\ W}{0.5\ m/s} = 480$ N。
(3) 不考虑滑轮组绳子的质量、滑轮与轴和绳子间的摩擦，由$\eta=\frac{W_{有用}}{W_{总}}=\frac{W_{有用}}{W_{有用}+W_{额外}}=\frac{Gh}{Gh + G_{动}h}=\frac{G}{G + G_{动}}$可得，动滑轮总重力：$G_{动}=\frac{G}{\eta}-G=\frac{480\ N}{80\%}-480\ N=120$ N。