第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
1. 下列图形中,对称轴最多的是(
A.角
B.等腰三角形
C.等边三角形
D.线段
C
)A.角
B.等腰三角形
C.等边三角形
D.线段
答案:
C
2. 如图,在△ABC中,AB= AC,DE是AB的垂直平分线,△BCE的周长为14,BC= 6,则AB的长为(
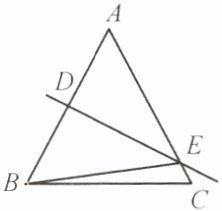
A.6
B.7
C.8
D.9
C
)
A.6
B.7
C.8
D.9
答案:
C
3. (1)已知等腰三角形的两边长分别是4 cm和9 cm,那么其周长为
(2)已知等腰三角形的周长为9 cm,一边长为4 cm,那么其腰长为
(3)已知等边三角形的边长为4 cm,那么它的周长为
22
cm。(2)已知等腰三角形的周长为9 cm,一边长为4 cm,那么其腰长为
4或2.5
cm。(3)已知等边三角形的边长为4 cm,那么它的周长为
12
cm。
答案:
(1) 22
(2) 4或2.5
(3) 12
(1) 22
(2) 4或2.5
(3) 12
4. 已知等腰三角形的周长是35 cm,腰长是底边的3倍,则这个等腰三角形的腰长是
15
cm。
答案:
15
5. 等腰三角形的底边长是8,则它的腰长x的取值范围是
$x > 4$
。
答案:
【解析】:
1. 设等腰三角形的腰长为 $x$,底边长为 8。
2. 根据三角形的三边关系,任意两边之和大于第三边,任意两边之差小于第三边。
3. 对于等腰三角形,两腰之和为 $2x$,腰与底边的差为 $x - 8$,腰与底边的和为 $x + 8$。
4. 应用三角形的三边关系,得到不等式:
$x + x > 8$
$2x > 8$
$x > 4$
同时,由于 $x - 8$ 必须小于 $x$(显然成立),且 $x + 8$ 必须大于 $x$(也显然成立),但关键是不等式 $2x > 8$。
5. 综上,得出 $x > 4$。
【答案】:由于题目要求的是取值范围,且为填空题,故答案应填为表示范围的符号或文字,本题答案填为“$x > 4$”对应的选项(在实际情况下,应直接写$x > 4$,若为选择题则根据选项选择对应答案,此处假设有对应选项则填对应选项字母)。由于本题返回格式要求,直接给出数学表达式答案。
答案:$x > 4$
1. 设等腰三角形的腰长为 $x$,底边长为 8。
2. 根据三角形的三边关系,任意两边之和大于第三边,任意两边之差小于第三边。
3. 对于等腰三角形,两腰之和为 $2x$,腰与底边的差为 $x - 8$,腰与底边的和为 $x + 8$。
4. 应用三角形的三边关系,得到不等式:
$x + x > 8$
$2x > 8$
$x > 4$
同时,由于 $x - 8$ 必须小于 $x$(显然成立),且 $x + 8$ 必须大于 $x$(也显然成立),但关键是不等式 $2x > 8$。
5. 综上,得出 $x > 4$。
【答案】:由于题目要求的是取值范围,且为填空题,故答案应填为表示范围的符号或文字,本题答案填为“$x > 4$”对应的选项(在实际情况下,应直接写$x > 4$,若为选择题则根据选项选择对应答案,此处假设有对应选项则填对应选项字母)。由于本题返回格式要求,直接给出数学表达式答案。
答案:$x > 4$
6. 有下列四种说法:①等腰三角形是轴对称图形。②等腰三角形的对称轴是顶角平分线。③等腰三角形的对称轴是顶角平分线所在的直线。④等腰三角形的对称轴有三条。其中正确的说法有
①③
。(填序号)
答案:
①③
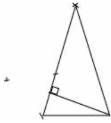
7. 已知线段a,b(如图)。用直尺和圆规作一个以a为底边,b为腰的等腰三角形,并画出一条腰上的高线。
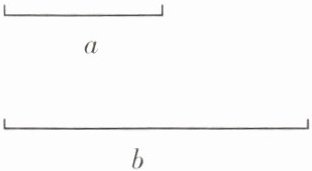
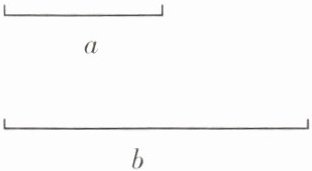
答案:

8. 下列说法正确的是(
A.等腰三角形的两条高相等
B.等腰三角形的两条角平分线相等
C.等腰三角形的两条中线相等
D.等腰三角形两腰上的中线相等
D
)A.等腰三角形的两条高相等
B.等腰三角形的两条角平分线相等
C.等腰三角形的两条中线相等
D.等腰三角形两腰上的中线相等
答案:
[解析]:
A. 对于等腰三角形,只有两腰上的高相等,而不是任意两条高都相等。底边上的高与腰上的高不一定相等。因此,A选项错误。
B. 对于等腰三角形,只有两个底角的角平分线相等,腰上的角平分线不一定相等。因此,B选项错误。
C. 对于等腰三角形,只有从两腰中点到对边的中线是相等的(即腰的中线),但底边的中线与腰的中线不一定相等。因此,C选项错误。
D. 对于等腰三角形,两腰上的中线是连接两腰的中点与对边顶点的线段,由于两腰长度相等,且中点将腰平分,因此两腰上的中线长度也相等。所以D选项正确。
[答案]:D
A. 对于等腰三角形,只有两腰上的高相等,而不是任意两条高都相等。底边上的高与腰上的高不一定相等。因此,A选项错误。
B. 对于等腰三角形,只有两个底角的角平分线相等,腰上的角平分线不一定相等。因此,B选项错误。
C. 对于等腰三角形,只有从两腰中点到对边的中线是相等的(即腰的中线),但底边的中线与腰的中线不一定相等。因此,C选项错误。
D. 对于等腰三角形,两腰上的中线是连接两腰的中点与对边顶点的线段,由于两腰长度相等,且中点将腰平分,因此两腰上的中线长度也相等。所以D选项正确。
[答案]:D
查看更多完整答案,请扫码查看


