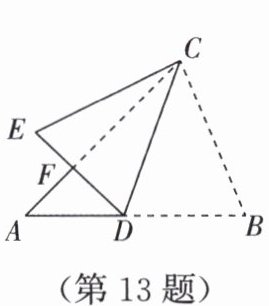
13. 如图,在 $\triangle ABC$ 中,点 $D$ 在 $AB$ 上,$\angle ACB = 70^{\circ}$,现将 $\triangle ABC$ 中的 $\angle B$ 折过去,使顶点 $B$ 落在点 $E$ 处,$CD$ 为折痕,且 $AC$ 交 $ED$ 于点 $F$,若 $\angle ECA = 20^{\circ}$,则 $\angle ACD$ 的大小为
25°
.
答案:
25°
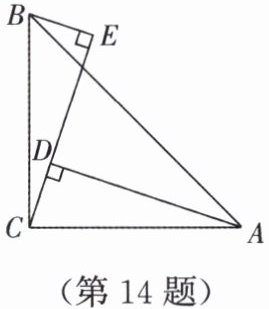
14. 如图,$\angle ACB = 90^{\circ}$,$AC = BC$,$AD \perp CE$,$BE \perp CE$,若 $AD = 3$,$BE = 1$,则 $DE$ 的长为
2
.
答案:
2
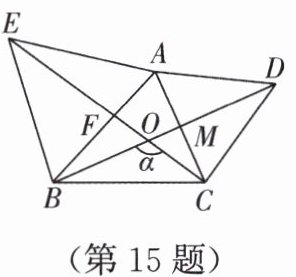
15. 如图,在锐角三角形 $ABC$ 外作等边三角形 $ACD$ 和等边三角形 $ABE$,则 $\angle \alpha$ 的大小为
120°
.
答案:
120°
16. 如图,$AB = 4\ cm$,$AC = BD = 3\ cm$,$\angle CAB = \angle DBA$,点 $P$ 在线段 $AB$ 上以 $1\ cm/s$ 的速度由点 $A$ 向点 $B$ 运动,同时,点 $Q$ 在线段 $BD$ 上由点 $B$ 向点 $D$ 运动. 若 $\triangle ACP$ 与 $\triangle BPQ$ 存在全等的情况,则点 $Q$ 的运动速度为

1或1.5
$cm/s$.
答案:
$1$或$1.5$
17. (本小题 8 分)
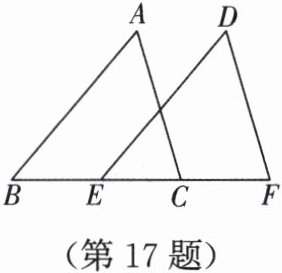
如图,已知点 $B$,$E$,$C$,$F$ 在同一条直线上,$AB = DE$,$\angle A = \angle D$,$AC // DF$. 求证 $BE = CF$.
如图,已知点 $B$,$E$,$C$,$F$ 在同一条直线上,$AB = DE$,$\angle A = \angle D$,$AC // DF$. 求证 $BE = CF$.

答案:
证明:
∵AC//DF,
∴∠ACB=∠DFE(两直线平行,内错角相等)。
在△ABC和△DEF中,
∠A=∠D(已知),
∠ACB=∠DFE(已证),
AB=DE(已知),
∴△ABC≌△DEF(AAS)。
∴BC=EF(全等三角形对应边相等)。
∵BC=BE+EC,EF=EC+CF,
∴BE+EC=EC+CF。
∴BE=CF(等式性质)。
∵AC//DF,
∴∠ACB=∠DFE(两直线平行,内错角相等)。
在△ABC和△DEF中,
∠A=∠D(已知),
∠ACB=∠DFE(已证),
AB=DE(已知),
∴△ABC≌△DEF(AAS)。
∴BC=EF(全等三角形对应边相等)。
∵BC=BE+EC,EF=EC+CF,
∴BE+EC=EC+CF。
∴BE=CF(等式性质)。
18. (本小题 8 分)
如图,方格纸上有一个 $\triangle ABC$,请你在方格纸内画出满足条件 $A_1B_1 = AB$,$B_1C_1 = BC$,$\angle A_1 = \angle A$ 的 $\triangle A_1B_1C_1$,并判断 $\triangle A_1B_1C_1$ 与 $\triangle ABC$ 是否一定全等.
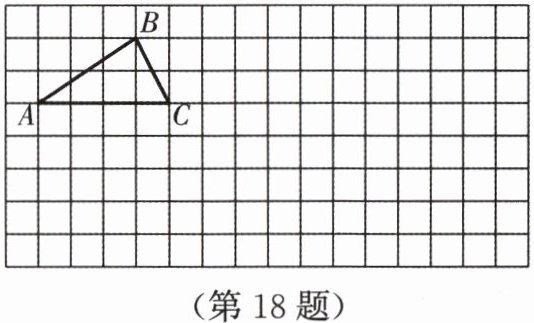
如图,方格纸上有一个 $\triangle ABC$,请你在方格纸内画出满足条件 $A_1B_1 = AB$,$B_1C_1 = BC$,$\angle A_1 = \angle A$ 的 $\triangle A_1B_1C_1$,并判断 $\triangle A_1B_1C_1$ 与 $\triangle ABC$ 是否一定全等.

答案:
$\triangle A_1B_1C_1$与$\triangle ABC$不一定全等。
查看更多完整答案,请扫码查看


