19. (本小题 10 分)
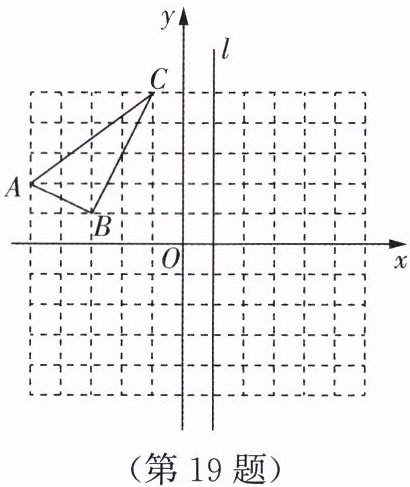
如图,在正方形网格中建立平面直角坐标系,$\triangle ABC的顶点坐标分别为A(-5,2)$,$B(-3,1)$,$C(-1,5)$.
(1)请你在图中画出$\triangle ABC关于y轴对称的图形A_1B_1C_1$,并写出点$B的对应点B_1$的坐标;
(2)如图,有平行于$y轴的直线l经过点(1,0)$,请你直接写出点$B关于直线l对称的点B_2$的坐标.
如图,在正方形网格中建立平面直角坐标系,$\triangle ABC的顶点坐标分别为A(-5,2)$,$B(-3,1)$,$C(-1,5)$.
(1)请你在图中画出$\triangle ABC关于y轴对称的图形A_1B_1C_1$,并写出点$B的对应点B_1$的坐标;
(2)如图,有平行于$y轴的直线l经过点(1,0)$,请你直接写出点$B关于直线l对称的点B_2$的坐标.

答案:
(1)
点$A(-5,2)$关于$y$轴对称的点$A_1$的坐标为$(5,2)$;
点$B(-3,1)$关于$y$轴对称的点$B_1$的坐标为$(3,1)$;
点$C(-1,5)$关于$y$轴对称的点$C_1$的坐标为$(1,5)$。
在坐标系中描出$A_1(5,2)$,$B_1(3,1)$,$C_1(1,5)$,并依次连接$A_1B_1$,$B_1C_1$,$C_1A_1$,得到$\triangle A_1B_1C_1$。
$B_1(3,1)$。
(2)
已知直线$l$平行于$y$轴且经过点$(1,0)$,则直线$l$的方程为$x = 1$。
点$B(-3,1)$到直线$x = 1$的距离为$\vert - 3 - 1\vert=4$,那么点$B$关于直线$l$对称的点$B_2$到直线$x = 1$的距离也为$4$,且在直线$l$右侧,所以$B_2$横坐标为$1 + 4=5$,纵坐标不变,即$B_2(5,1)$。
综上,答案依次为:
(1)图略(按上述描点连线操作);$B_1(3,1)$;
(2)$B_2(5,1)$。
(1)
点$A(-5,2)$关于$y$轴对称的点$A_1$的坐标为$(5,2)$;
点$B(-3,1)$关于$y$轴对称的点$B_1$的坐标为$(3,1)$;
点$C(-1,5)$关于$y$轴对称的点$C_1$的坐标为$(1,5)$。
在坐标系中描出$A_1(5,2)$,$B_1(3,1)$,$C_1(1,5)$,并依次连接$A_1B_1$,$B_1C_1$,$C_1A_1$,得到$\triangle A_1B_1C_1$。
$B_1(3,1)$。
(2)
已知直线$l$平行于$y$轴且经过点$(1,0)$,则直线$l$的方程为$x = 1$。
点$B(-3,1)$到直线$x = 1$的距离为$\vert - 3 - 1\vert=4$,那么点$B$关于直线$l$对称的点$B_2$到直线$x = 1$的距离也为$4$,且在直线$l$右侧,所以$B_2$横坐标为$1 + 4=5$,纵坐标不变,即$B_2(5,1)$。
综上,答案依次为:
(1)图略(按上述描点连线操作);$B_1(3,1)$;
(2)$B_2(5,1)$。
20. (本小题 10 分)
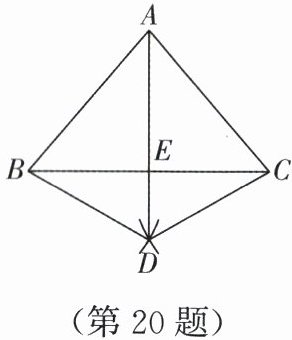
如图,在$\triangle ABC$中,$AB = AC$,分别以$B$,$C$为圆心,大于$\frac{1}{2}BC$的长为半径作弧,两弧交于点$D$,连接$BD$,$CD$,$AD$,$AD与BC交于点E$.
(1)求证$\triangle ABD \cong \triangle ACD$;
(2)若$BD = 2$,$\angle BDC = 120^{\circ}$,求$DE$的长.
如图,在$\triangle ABC$中,$AB = AC$,分别以$B$,$C$为圆心,大于$\frac{1}{2}BC$的长为半径作弧,两弧交于点$D$,连接$BD$,$CD$,$AD$,$AD与BC交于点E$.
(1)求证$\triangle ABD \cong \triangle ACD$;
(2)若$BD = 2$,$\angle BDC = 120^{\circ}$,求$DE$的长.

答案:
(1) 见解析;
(2) $DE=1$
(1) 见解析;
(2) $DE=1$
查看更多完整答案,请扫码查看


