13. 已知$y^{2}+my + 4$是完全平方式,则$m$的值是
$\pm4$
.
答案:
$\pm4$
14. 如图,$\angle 1是\triangle ABC$的一个外角,若$\angle 1 = 85^{\circ}$,$\angle C = 30^{\circ}$,则$\angle B = $
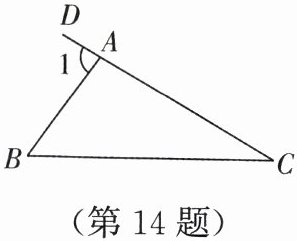
55°
.
答案:
55°
15. 方程$\frac{1}{x - 3}+2= \frac{1 - x}{x - 3}$的解是
$x = 2$
.
答案:
$x = 2$
16. 在$\triangle ABC$中,若$AB - AC = 2\ cm$,$BC的垂直平分线交AB于点D$,且$\triangle ACD$的周长为 14 cm,则$AB = $
8
.
答案:
8
17. 如图,等腰三角形$ABC底边BC$的长为 4,面积是 12,$D为BC$边上的中点,腰$AB的垂直平分线EF交AD于点M$,交$AC于点F$,则$BM + DM$的值为______.
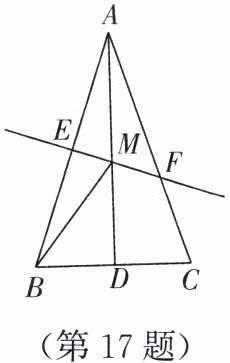

6
答案:
6
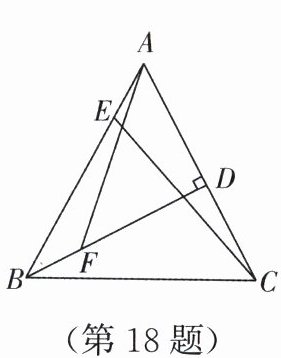
18. 如图,$AB = AC$,$BD\perp AC于点D$,$E$,$F分别为AB$,$BD$上的动点,且$AE = BF$,$\angle DBA = 34^{\circ}$.
(1)试判断$CE与BD$的大小关系:$CE$
(2)当$CE + AF$取得最小值时,$\angle BEC$的度数是
(1)试判断$CE与BD$的大小关系:$CE$
≥
$BD$(填“$\geqslant$”或“$\leqslant$”);(2)当$CE + AF$取得最小值时,$\angle BEC$的度数是
101°
.
答案:
(1)≥;
(2)101°
(1)≥;
(2)101°
19. (本小题 8 分)
计算:
(1)$(2x + 3y)(2x - y)$; (2)$(3a^{2}b^{3}-a^{3}b^{4})÷(-2a^{2}b^{2})$;
(3)$(a + 1)^{2}-(a - 1)(a + 3)$; (4)$\frac{1 - x}{2x - 4}÷(x + 2+\frac{3}{x - 2})$.
计算:
(1)$(2x + 3y)(2x - y)$; (2)$(3a^{2}b^{3}-a^{3}b^{4})÷(-2a^{2}b^{2})$;
(3)$(a + 1)^{2}-(a - 1)(a + 3)$; (4)$\frac{1 - x}{2x - 4}÷(x + 2+\frac{3}{x - 2})$.
答案:
(1)
$\begin{aligned}&(2x + 3y)(2x - y)\\=&2x×2x-2x× y + 3y×2x-3y× y\\=&4x^{2}-2xy + 6xy-3y^{2}\\=&4x^{2}+4xy - 3y^{2}\end{aligned}$
(2)
$\begin{aligned}&(3a^{2}b^{3}-a^{3}b^{4})÷(-2a^{2}b^{2})\\=&3a^{2}b^{3}÷(-2a^{2}b^{2})-a^{3}b^{4}÷(-2a^{2}b^{2})\\=&-\frac{3}{2}b+\frac{1}{2}ab^{2}\end{aligned}$
(3)
$\begin{aligned}&(a + 1)^{2}-(a - 1)(a + 3)\\=&a^{2}+2a + 1-(a^{2}+3a-a - 3)\\=&a^{2}+2a + 1 - a^{2}-2a + 3\\=&4\end{aligned}$
(4)
$\begin{aligned}&\frac{1 - x}{2x - 4}÷(x + 2+\frac{3}{x - 2})\\=&\frac{1 - x}{2(x - 2)}÷\frac{(x + 2)(x - 2)+3}{x - 2}\\=&\frac{1 - x}{2(x - 2)}÷\frac{x^{2}-4 + 3}{x - 2}\\=&\frac{1 - x}{2(x - 2)}÷\frac{x^{2}-1}{x - 2}\\=&\frac{1 - x}{2(x - 2)}×\frac{x - 2}{(x + 1)(x - 1)}\\=&-\frac{1}{2(x + 1)}\end{aligned}$
(1)
$\begin{aligned}&(2x + 3y)(2x - y)\\=&2x×2x-2x× y + 3y×2x-3y× y\\=&4x^{2}-2xy + 6xy-3y^{2}\\=&4x^{2}+4xy - 3y^{2}\end{aligned}$
(2)
$\begin{aligned}&(3a^{2}b^{3}-a^{3}b^{4})÷(-2a^{2}b^{2})\\=&3a^{2}b^{3}÷(-2a^{2}b^{2})-a^{3}b^{4}÷(-2a^{2}b^{2})\\=&-\frac{3}{2}b+\frac{1}{2}ab^{2}\end{aligned}$
(3)
$\begin{aligned}&(a + 1)^{2}-(a - 1)(a + 3)\\=&a^{2}+2a + 1-(a^{2}+3a-a - 3)\\=&a^{2}+2a + 1 - a^{2}-2a + 3\\=&4\end{aligned}$
(4)
$\begin{aligned}&\frac{1 - x}{2x - 4}÷(x + 2+\frac{3}{x - 2})\\=&\frac{1 - x}{2(x - 2)}÷\frac{(x + 2)(x - 2)+3}{x - 2}\\=&\frac{1 - x}{2(x - 2)}÷\frac{x^{2}-4 + 3}{x - 2}\\=&\frac{1 - x}{2(x - 2)}÷\frac{x^{2}-1}{x - 2}\\=&\frac{1 - x}{2(x - 2)}×\frac{x - 2}{(x + 1)(x - 1)}\\=&-\frac{1}{2(x + 1)}\end{aligned}$
查看更多完整答案,请扫码查看


